how i can find mathematical way to know the number of triangles are in this photo?
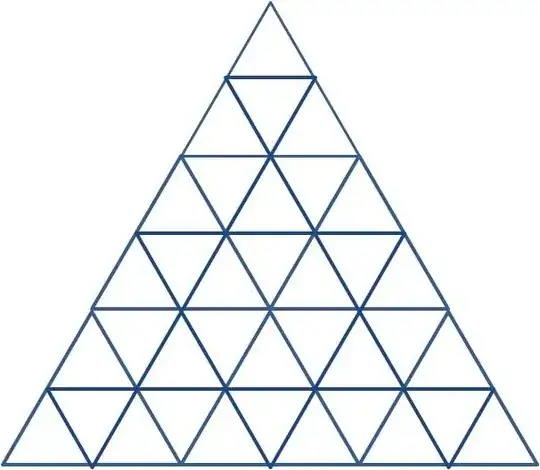
I sure that the solution like sequence or series but how to find it ?
if I added new line so what is the number of triangles become?
thanks for all
how i can find mathematical way to know the number of triangles are in this photo?

I sure that the solution like sequence or series but how to find it ?
if I added new line so what is the number of triangles become?
thanks for all
Any triangle either has a top most vertex, or a bottom most vertex.
First, count triangles with a top most vertex. Starting from the vertex at the top we have $6$ possible triangles. The two vertices in the second row each have $5$ possible triangles, and so on.
The pattern continues:
$$1\cdot6+2\cdot5+3\cdot4+4\cdot3+5\cdot2+6\cdot1=56$$
Next, count triangles with a bottom most vertex. Starting with the vertices at the bottom, there are $1+2+3+2+1=9$ such triangles. In the second row from the bottom, there are $1+2+2+1=6$ such triangles. Continuing we get $1+2+1=4$ and $1+1=2$ for the next two rows, finishing with $1$ near the top. This gives us $22$ triangles with a lower most vertex.
Altogether, we have $78$ triangles.