Equation to place points equidistantly on an Archimedian Spiral using arc-length

Question

I am looking for a way to place points equidistantly along an Archimedes spiral according to arch-length (or an approximation) given the following parameters:

Max Radius, Fixed distance between the points, Number of points

I have been lurking around on this site for a few days and have found a lot of great advice but am struggling with the syntax of some of the proposed responses (not a native coder but I have had small exposure to Python and Matlab).

This example 1 seems to be exactly what I am looking for but I am just struggling with the code, it is not clear to me what variables are used or how the program executes.

Example 2 and example 3 were also helpful but I am definitely missing something when it comes to solving the equation numerically as the resulting spiral does not have equal spacing.

My goal is to use a spreadsheet (MS Excel) to drive a solid modeling program to generate a hole pattern per the parameters above.

Cheers!

Answer 1

I've taken a different approach, which, while requiring an extra step is ultimately a better approximation to an equi-spaced curve. In the complex plane, we know that the arc length is given by

$$s=\int_0^{\theta}|\dot z|d\theta$$

where $\dot z$ means differentiation w.r.t. $\theta$ in this case. The for range of $[\theta:\theta+\Delta \theta]$ we can say

$$\Delta s=\int_{\theta}^{\theta+\Delta \theta}|\dot z|d\theta\approx \frac{|\dot z|_n+|\dot z|_{n+1}}{2}\Delta \theta$$

So, the extra step I mentioned consists of building successive $\theta_n$ from $\theta_{n-1}$. For Archimedes spiral $|\dot z|=\sqrt{1+\theta^2}$ and we can show that

$$\Delta \theta_n\approx\frac{\Delta s}{\sqrt{1+\theta_n^2}}$$

The figure below shows a comparison of the uniform $\theta$ (left) and uniform $s$ (right). I kept the derivation very general up to the last minute because it applies to any curve, obviously. .

Answer 2

If the polar equation of an Archimedean spiral is given by: $$ \rho = \theta $$ then its parametric equation is $(\theta\cos\theta,\theta\sin\theta)$ and the arc length between $0$ and $\theta_f$ is given by: $$ L= \int_{0}^{\theta_f}\sqrt{1+\theta^2}\,d\theta = \frac{1}{2}\left(\theta_f \sqrt{1+\theta_f^2}+\text{arcsinh}(\theta_f)\right)\approx \theta_f \sqrt{1+\frac{\theta_f^2}{4}}$$ so a good way to place almost-equispaced point on such Archimedean spiral is to take the $N$-th point at: $$ \theta_N = \sqrt{2}\sqrt{-1+\sqrt{1+k^2 N^2}}. $$

Answer 3

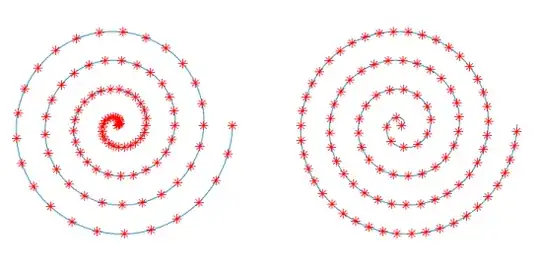
A python implementation to solve for evenly spaced points around an Archimedean spiral. Most of the solutions I came across assume $a=0$ so here is my solution which does not ignore $a$.

Use a solver to iteratively find $\theta_b$ that satisfies:

$\text{arc length} = s = \int_{\theta_a}^{\theta_b} \sqrt{(\frac{dr}{d\theta})^2 + r^2}$ when $r = a+b\theta$
https://en.wikipedia.org/wiki/Arc_length#Other_coordinate_systems

$\therefore s = \int_{\theta_a}^{\theta_b} \sqrt{b^2 + (a+b\theta)^2}$

Using Sage to integrate:
$s = \frac{b^{2} \operatorname{arsinh}\left(\frac{b \theta_{b} + a}{b}\right) + \sqrt{b^{2} \theta_{b}^{2} + 2 \, a b \theta_{b} + a^{2} + b^{2}} {\left(b \theta_{b} + a\right)}}{2 \, b} -\frac{b^{2} \operatorname{arsinh}\left(\frac{b \theta_{a} + a}{b}\right) + \sqrt{b^{2} \theta_{a}^{2} + 2 \, a b \theta_{a} + a^{2} + b^{2}} {\left(b \theta_{a} + a\right)}}{2 \, b} $

Scipy's fsolve searches for roots where func(x) = 0. So subtract $s$ (the requested arc length) from both sides and solve for the $\theta_b$ where $\text{func}(\theta_b) \approx 0$.

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import fsolve
def arc_len(theta_b: float, theta_a: float, a: float, b: float, arclen: float):
    """calculated arc_len between theta_a and theta_b (where theta_b > theta_a) minus requested arclen
Args:
    theta_b (float): upper bound for arc
    theta_a (float): lower bound for arc
    a (float): from the definition of an archimedean spiral r = a + b * theta
    b (float): from the definition of an archimedean spiral r = a + b * theta
    arclen (float): the goal arc length

Returns:
    float: arclen from theta_a to theta_b minus requested arc length

Arc length definition:
https://en.wikipedia.org/wiki/Arc_length#Other_coordinate_systems

using sagemath: https://www.sagemath.org/
sage: arclen, a, b, t, theta_a, theta_b = var('arclen a b t theta_a theta_b')
sage: integral((b^2 + (a + b*t)^2)^0.5, t, theta_a,theta_b, assume(a>0,b>0,theta_b-theta_a>0)).simplify()

.. math::
    -\frac{b^{2} \operatorname{arsinh}\left(\frac{b \theta_{a} + a}{b}\right) + \sqrt{b^{2} \theta_{a}^{2} + 2 \, a b \theta_{a} + a^{2} + b^{2}} {\left(b \theta_{a} + a\right)}}{2 \, b} + \frac{b^{2} \operatorname{arsinh}\left(\frac{b \theta_{b} + a}{b}\right) + \sqrt{b^{2} \theta_{b}^{2} + 2 \, a b \theta_{b} + a^{2} + b^{2}} {\left(b \theta_{b} + a\right)}}{2 \, b}

"""

return (1 / (2 * b)) * (
    (
        b**2 * np.arcsinh((b * theta_b + a) / b)
        + np.sqrt(b**2 * theta_b**2 + 2 * a * b * theta_b + a**2 + b**2)
        * (b * theta_b + a)
    )
    - (
        b**2 * np.arcsinh((b * theta_a + a) / b)
        + np.sqrt(b**2 * theta_a**2 + 2 * a * b * theta_a + a**2 + b**2)
        * (b * theta_a + a)
    )
) - arclen



def main():
    # archimedean spiral definition r = a + btheta
    a = 3
    b = 1 / (2  np.pi)
    turns = 3
# requested arc length
arclen = 7

theta = 0
max_theta = turns * 2 * np.pi

thetas = []

while theta < max_theta:
    theta = fsolve(arc_len, [theta], args=(theta, a, b, arclen,))[0]
    thetas.append(theta)

# ignore the last calculated point (Outside of the requested range)
thetas = np.array(thetas[:-1])

################ PLOTTING ################
### polar ###
fig = plt.figure(figsize=(6,3))
ax0 = plt.subplot(121, polar=True, aspect="equal")

# calculated points
r_div = a + b * thetas
ax0.scatter(thetas, r_div, color="#a65628", zorder=2)

# spiral line
theta = np.arange(0, turns * 2 * np.pi + 0.001, np.pi / 32)
r = a + b * theta
ax0.plot(theta, r, color="#377eb8", zorder=1)

### cartesian ###
ax1 = plt.subplot(122, aspect="equal")

x = r_div * np.cos(thetas)
y = r_div * np.sin(thetas)

# calculated points
ax1.scatter(x, y, color="#a65628", zorder=2)

x = r * np.cos(theta)
y = r * np.sin(theta)

# spiral line
ax1.plot(x, y, color="#377eb8", zorder=1)

plt.tight_layout()
plt.show()



if name == "main":
    main()

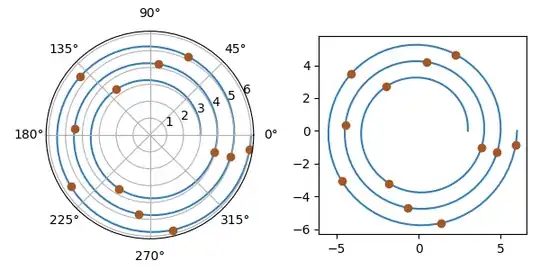
Plotted in both polar and Cartesian, the brown points here are spaced evenly (with an arc length = 7) around the spiral $r = 3 + \frac{1}{2\pi}\theta$