How many squares can be packed on a spiral?

Question

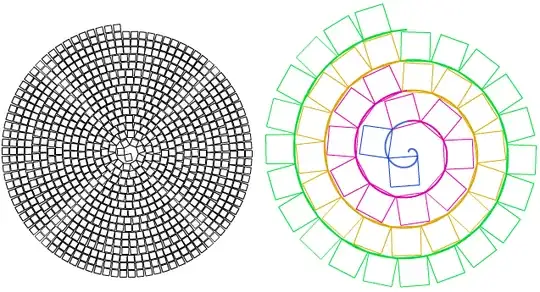
Given an Archimedean Spiral, what's the maximal number of squares of maximal size you can pack onto it for the first $n$ turns?

Squares are packed in a way such that each square can touch the spiral with only 2 corner points of the same side. All squares are connected in a chain in those corner points.

Maximal size means that a set of "a bit bigger" squares won't fit to be packed in this way.

Some images I sketched:

The right one is colored each turn in other color ($n=4$). The sides of the squares are around the same size as the distance between the turnings: approximation as I'm not sure how to find the exact size of the side of the maximal squares.

If the colorful sketch is correct: then for first four turns ($n$s), we have: $2, 12, 28, 50$ squares.

---

Can this be mathematically calculated for some $n$? I have no idea where to start but to explore these approximation sketches I'm drawing. I haven't yet been introduced to spirals or polar coordinate systems so I'm in the dark here. This question just popped in my head when I saw stone tiles arranged as sketch on the left.

Answer 1

Frankly, I don't think you will find a totally satisfactory answer to your question because of the vagaries in the vicinity of the origin. Another problem is that when you plot the spiral as a function of $\theta$ the points are not spaced evenly. The final problem is that this would be very difficult in to do in Cartesian coordinates, difficult in polar coordinates, but relatively easy in complex variables, which you have indicated you have not yet reached in your studies.

Nevertheless, let me show you how I approached the problem. The equation for Archimedes spiral in complex variables is

$$z=a~\theta~e^{i\theta}$$

In a previous post here, I showed how to create evenly-spaced points on the spiral, Bear in mind that this is approximate.

For the present problem I chose $a=1/2\pi$ in order to get unit spacing of the spiral on consecutive turns. Applying my method for unit spacing on the spiral I get the curve on the left in the figure below. The reconfigured spacing is shown in red stars. The for every pair of stars I can create the squares shown on the left. This too, is relatively straightforward in complex variables, easy, in fact. The spiral was created in the range $\theta\in[0,10\pi]$ while for the squares $\theta\approx[0,8\pi]$.

The program I generated can go out to any values of $\theta$. I stopped here in order to keep the figures understandable.

In order to determine how may squares can fit in each loop you are going to have to be able compute the arc length. This can be accomplished with

$$ s=\int |\dot z|~du\\ \text{or}\\ s=\int \sqrt{1+\left(\frac{dy}{dx} \right)^2}~dx $$

There is a lot going on here, but I hope that it's a start to answering your question.