So I am doing this coding project for fun ;
I have a set of $n$ particles of diameter $d$ scattered across the screen on the canvas. By clicking a button I want them to rearrange into a Fibonacci spiral.
To achieve this, I need to, given $c = (c_{x}, c_{y})$ the center coordinates of the screen, to generate a set of $n$ $2$-dimensional coordinates representing the sequence defining a Fibonacci spiral. Each point should be spaced such that there is $\sim d$ distance between one another (to allocate space for the particles).
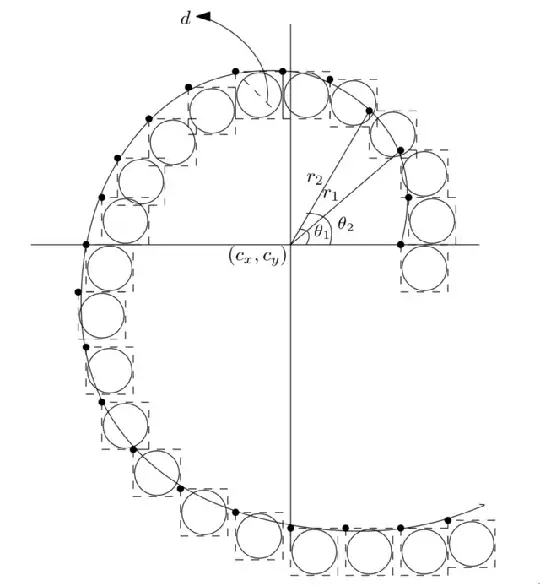
Here is a picture I drew to illustrate what I am trying to achieve
Things I have done
So far I am quite stuck on the premisse.I think I need to find a relationship on how $\theta$ is growing at after every coordinate such that I could generate my coordinates with $x = e^{\theta} \cos \theta$ and $y = e^{\theta} \sin \theta$. Given the figure above, let $\alpha = \theta_2 - \theta_1$. $r_1$ can be known from the base case (if it were a straight line on the $x$ axis then it would be $r_{1} = (1.618,0)$), but $r_{2}$ is not necessarely known. Using the Law of Cosines $$ d^2 \approx r_{2}^2 + r_{1}^2 - 2r_{2}r_{1} \cos \alpha,$$ but then also, setting $a=b$ in $r = ae^{b\theta}$ for simplicity, $$ r = e^{\theta} \implies \theta_2 - \theta_1 = \alpha = \log\left( \frac{r_{2}}{r_{1}}\right).$$ I am not sure how to manipulate these equations to find what I am looking for, I am stuck.
Does anyone have any hints or ideas on how I could proceed with this problem?