Trying to obtain a better bound for a problem from this bounty question, I obtained the following problem. Let $n\ge 3$ be a natural number. The problem is to estimate (in particular, asymptotically) a function $f(n)$ which is the largest number such that for each $n$-element set $A$ of natural numbers there exist different pairs $\{a,c\}$ and $\{b,d\}$ of different numbers from the set $A$, such that $$\left|\dfrac{1}{a}+\dfrac{1}{c}-\dfrac{1}{b}-\dfrac{1}{d}\right|\le\dfrac 1{f(n)}.$$
My try. :-) It seems the following.
Without loss of generality, we can assume that all sums $\frac 1a+\frac 1b$ for numbers $a<b$ from the set $A$ are distinct. Let $1\le k\le n-4$ and a set $A’$ consists of the $n-k$ biggest integers from $A$. For each pair of different numbers $a,b$ from the set $A’$ we have $\dfrac{1}{a}+\dfrac{1}{b}\le \dfrac{1}{k+1}+\dfrac{1}{k+2}.$ Also there are ${n-k \choose 2}$ different pairs of different numbers $a,b$ from the set $A’$. Therefore the set $S=\left\{\dfrac{1}{a}+\dfrac{1}{b}:x,y\in A’\right\}$ consists of $M$ points which belong to an interval $\left[0; \dfrac{1}{k+1}+\dfrac{1}{k+2}\right]$ of length $\dfrac{1}{k+1}+\dfrac{1}{k+2}.$ Therefore there exist two different points of the set $S$ with distance between them at most $\frac{\dfrac{1}{k+1}+\dfrac{1}{k+2}}{M-1}.$ When we take a suitable value of $k$ this gives an asymptotical lower bound for $f(n)$ of order $n^3$.
On the other hand, it is easy to see that a set $A=\{1,p_1,\dots, p_{n-1}\}$, where $p_i$ is the $i$-th prime number provides a bound $f(n)< p_n^4<(n(\log n+\log\log n))^4$ for each $n\ge 6$, see here.
But maybe applying some number theoretic facts we can obtain an (asymptotically) better lower bound for $f(n)$, and using more subtle construction we can obtain an (asymptotically) better upper bound for $f(n)$.
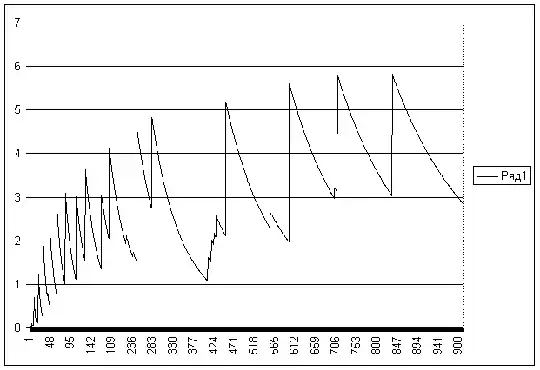
Update. I wrote a program which provides a bound $g(n)\ge f(n)$ starting from $a_1=1$ and greedily taking by $a_n$ the smallest natural number such that all values $1/a_i+1/a_j-1/a_k-1/a_n$ for $1\le i,j,k<n$ are non-zero. See the graph of $g(n)/n^4$ for $2\le n\le 1000$.