This question is related to an upper bound for a problem from my five-year-old question.
Let $n\ge 3$ be a natural number and $A_n$ be a set consisting of $1$ and first $n-1$ prime numbers. We want to asymptotically estimate the smallest non-zero absolute value $\frac 1{g(n)}$ of a number $\tfrac{1}{a}+\tfrac{1}{c}-\tfrac{1}{b}-\tfrac{1}{d}$ where $a,b,c,d\in A_n$.
Reducing the sum of reciprocal to a common denominator, it is easy to show that
$$g(n)<p_{n-1}^4<p_n^4<(n(\log n+\log\log n))^4$$ for each $n\ge 6$, see here, where $p_{n-1}$ is $(n-1)$-th prime number.
Question. (by mathworker21) Can we improve this asymptotic upper bound for $g(n)$? More precisely, can we replace $(\log n)^4+O((\log n)^4)$ multiplier by a smaller one?
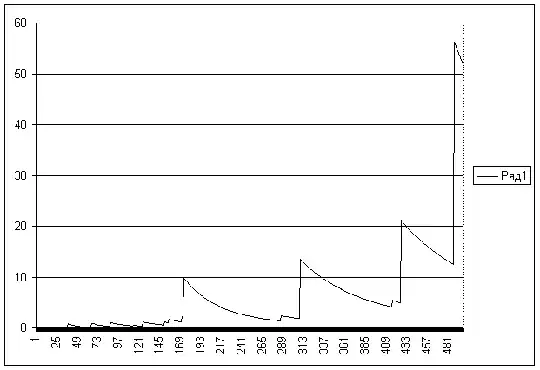
I wrote a program which calculated values of $g(n)/n^4$ for $n\le 500$, see the graph.
It is hard to guess an answer to the question due to splashes of $g(n)$. The first big splash is at $n=150$ due to $$\frac 1{457}+\frac 1{859}-\frac 1{503}-\frac 1{753}\approx 10^{-10}.$$ The biggest splach is at $n=452$ due to $$\frac 1{1823}+\frac 1{3187}-\frac 1{1979}-\frac 1{2801}\approx 3\cdot 10^{-13}.$$
PS. Similar bounds with the set $A_n$ replaced by the set $A'_n=\{1,2,3,4,5,7,\dots\}$ of prime powers also fit for my purposes.
The graph of the counterpart of the function $g(n)/n^4$ for $n\le 500$.
Thanks.