Fourier transform of $\left|\frac{\sin x}{x}\right|$

Question

Is there a closed form (possibly, using known special functions) for the Fourier transform of the function $f(x)=\left|\frac{\sin x}{x}\right|$?

$\hspace{.7in}$

I tried to find one using Mathematica, but it ran for several hours without producing any result.

Answer 1

Since $\left|\frac{\sin(x)}{x}\right|$ is not in $L^1$, there is no Fourier transform in the strict sense. However, we can get a Fourier transform in the sense of distributions (via Plancherel's Theorem).

The standard result about the sinc function is that $$ \int_{-\infty}^\infty\frac{\sin(ax)}{ax}e^{-2\pi ix\xi}\,\mathrm{d}x =\frac\pi{a}\left[|\xi|\le\frac{a}{2\pi}\right]\tag{1} $$ where $[\,\cdot\,]$ are Iverson brackets. $$ \int_{-\infty}^\infty\frac{\sin(2(k+1)\pi^2x)-\sin(2k\pi^2x)}{\pi x}e^{-2\pi ix\xi}\,\mathrm{d}x =\Big[k\pi\le|\xi|\le (k+1)\pi\Big]\tag{2} $$ Note that $$ \mathrm{sgn}\left(\frac{\sin(x)}{x}\right)=\sum_{k=0}^\infty(-1)^k\Big[k\pi\le|\xi|\le (k+1)\pi\Big]\tag{3} $$ Combining $(2)$ and $(3)$ yields the Fourier transform of $\mathrm{sgn}\left(\frac{\sin(x)}{x}\right)$ in the sense of distributions $$ \begin{align} &\sum_{k=0}^\infty(-1)^k\frac{\sin(2(k+1)\pi^2x)-\sin(2k\pi^2x)}{\pi x}\\ &=\frac2{\pi x}\sum_{k=0}^\infty(-1)^k\sin(2(k+1)\pi^2x)\\ &=\frac{\tan(\pi^2x)}{\pi x}\tag{4} \end{align} $$ Since the Fourier transform of a product is the convolution of the Fourier transforms, the Fourier transform of $\left|\frac{\sin(x)}{x}\right|$ is the convolution $$ \left[|\xi|\le\frac1{2\pi}\right]\ast\frac{\tan(\pi^2\xi)}{\xi} =\mathrm{PV}\int_{\xi-\frac1{2\pi}}^{\xi+\frac1{2\pi}}\frac{\tan(\pi^2t)}{t}\,\mathrm{d}t\tag{5} $$ using the Cauchy Principal Value in $(5)$.

---

Plots of the Fourier Transform:

$\hspace{8mm}$

$\hspace{5mm}$

Answer 2

$\newcommand{\abs}[1]{\left\vert #1\right\vert}% \newcommand{\ic}{{\rm i}}$ We didn't calculate the Fourier transform the OP asked for. We just calculate its derivative. It turns out that it has singularities at $k =0, \pm 1, \pm 2, \pm 4, \pm 6,\ldots$. We believe this is the root of problems which makes hard to evaluates the Fourier transform mentioned above. We hope somebody else can take from our final result.

\begin{align} \phi\left(k\right) &\equiv \int_{-\infty}^{\infty}\abs{\sin\left(x\right) \over x}\,{\rm e}^{-\ic kx} \,{\rm d}x = 2\int_{0}^{\infty}{\abs{\sin\left(x\right)} \over x}\,\cos\left(kx\right) \,{\rm d}x \\[3mm] \phi'\left(k\right) &= -2\int_{0}^{\infty}\abs{\sin\left(x\right)}\sin\left(kx\right) \,{\rm d}x\,, \end{align}

$\abs{\sin\left(x\right)}\quad$ is periodic $\left(~\mbox{of period}\ \pi~\right)$: $\abs{\sin\left(x\right)} = \sum_{n = -\infty}^{\infty}A_{n}\cos\left(2nx\right)$ with $$ \int_{-\pi/2}^{\pi/2}\cos\left(2mx\right)\cos\left(2nx\right)\,{\rm d}x = {\pi \over 2}\,\delta_{mn} $$

$$ A_{n} = {2 \over \pi}\int_{-\pi/2}^{\pi/2}\abs{\sin\left(x\right)}\cos\left(2nx\right) \,{\rm d}x = {4 \over \pi}\,{1 \over 1 - 4n^{2}} = -\,{1 \over \pi}\,{1 \over n^{2} - 1/4} $$

Then,

\begin{align} \phi'\left(k\right) &= -2\sum_{n = -\infty}^{\infty}A_{n}\int_{0}^{\infty}\cos\left(2nx\right)\sin\left(kx\right) \,{\rm d}x \\[3mm]&= -\,\Im\sum_{n = -\infty}^{\infty} A_{n}\int_{0}^{\infty}\left[% {\rm e}^{\ic\left(k - 2n\right)x} + {\rm e}^{\ic\left(k + 2n\right)x} \right]\,{\rm d}x \\[3mm]&= -\,\Im\sum_{n = -\infty}^{\infty}A_{n}\left[% {-1 \over \ic\left(k - 2n\right) - 0^{+}} + {-1 \over \ic\left(k + 2n\right) - 0^{+}} \right] \\[3mm]&= -\,\Im\sum_{n = -\infty}^{\infty}A_{n}\left(% {-\ic \over 2n - k - \ic 0^{+}} + {\ic \over 2n + k + \ic 0^{+}} \right) \\[3mm]&= {1 \over 2}\Re\sum_{n = -\infty}^{\infty}A_{n}\left(% {1 \over n - k/2 - \ic 0^{+}} - {1 \over n + k/2 + \ic 0^{+}} \right) \\[3mm]&= -\,{1 \over 2\pi}{\cal P}\,k\sum_{n = -\infty}^{\infty} {1 \over n^{2} - 1/4}\,{1 \over n^{2} - \left(k/2\right)^{2}} \\[3mm]&= -\,{1 \over 2\pi}{\cal P}\,\left[% {16 \over k} + 2k\sum_{n = 0}^{\infty} {1 \over n^{2} - 1/4}\,{1 \over n^{2} - \left(k/2\right)^{2}} \right] \\[3mm]&= -\,{1 \over 2\pi}{\cal P}\,\left\{% {16 \over k} - {8k \over k^{2} - 1}\sum_{n = 0}^{\infty}\left[% {1 \over n^{2} - 1/4} - {1 \over n^{2} - \left(k/2\right)^{2}} \right]\right\} \end{align}

\begin{align} \sum_{n = 0}^{\infty}{1 \over n^{2} - a^{2}} &= \sum_{n = 0}^{\infty}{1 \over \left(n + \abs{a}\right)\left(n - \abs{a}\right)} = {\Psi\left(\abs{a}\right) - \Psi\left(-\abs{a}\right) \over 2\abs{a}} \\[3mm]&= {1 \over 2\abs{a}}\left\{% \Psi\left(\abs{a}\right) - \Psi\left(1 + \abs{a}\right) + \pi\cot\left(\pi\left[-\abs{a}\right]\right) \right\} = {1 \over 2\abs{a}}\left[% -\,{1 \over \abs{a}} - \pi\cot\left(\pi\abs{a}\right) \right] \end{align}

$$ \sum_{n = 0}^{\infty}{1 \over n^{2} - a^{2}} = -\,{1 \over 2a^{2}}\left[% 1 + {\pi a \over \tan\left(\pi a\right)}\right]\,, \qquad a \not\in {\mathbb Z} $$

$$ \sum_{n = 0}^{\infty}{1 \over n^{2} - 1/4} = -2\,, \qquad \sum_{n = 0}^{\infty}{1 \over n^{2} - \left(k/2\right)^{2}} = -\,{2 \over k^{2}}\left[1 + {\pi k/2 \over \tan\left(\pi k/2\right)}\right] $$

\begin{align} \phi'\left(k\right) &= -\,{1 \over 2\pi}{\cal P}\,\left[% {16 \over k} + {16k \over k^{2} - 1} - {16 \over k}\,{1 \over k^{2} - 1} - {16 \over k}\,{1 \over k^{2} - 1}\,{\pi k/2 \over \tan\left(\pi k/2\right)} \right] \end{align}

\begin{align} \phi'\left(k\right) &= -\,{1 \over 2\pi}{\cal P}\,\left[% {32k \over k^{2} - 1} - {16 \over k}\,{1 \over k^{2} - 1}\,{\pi k/2 \over \tan\left(\pi k/2\right)} \right] \end{align}

We can observe that $\phi'\left(k\right)$ diverges at $k$ values: $$ k = 0, \pm 1, \pm 2, \pm 4, \pm 6,\ldots $$

Answer 3

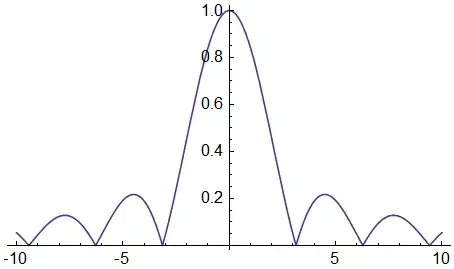
The function

$$f(x)=|\text{sinc}(x)|\tag{1}$$

can be evaluated as

$$f(x)=g_1(x)\, h_1(x)\tag{2}$$

where

$$g_1(x)=\left|\frac{1}{x}\right|\tag{3}$$

and

$$h_1(x)=|\sin(x)|\tag{4}$$

---

Therefore the Fourier transform

$$\hat{f}(\omega)=\mathcal{F}_x[f(x)](\omega)=\int\limits_{-\infty}^{\infty} f(x)\, e^{-2 \pi i \omega x} \, dx\tag{5}$$

can be evaluated as the convolution

$$[\hat{g}_1(\xi) * \hat{h}_1(\xi)](\omega)=\int\limits_{\infty}^{\infty} \hat{g}_1(\xi)\, \hat{h}_1(\omega-\xi) \, d\xi\tag{6}$$

where

$$\hat{g}_1(\omega)=\mathcal{F}_x[g_1(x)](\omega)=-2 (\log(2 \pi |\omega|)+\gamma)\tag{7}$$

is the Fourier transform of $g_1(x)$ and $\hat{h}_1(\omega)=\mathcal{F}_x[h_1(x)](\omega)$ is the Fourier transform of $h_1(x)$.

---

The function $h_1(x)$ is a $\pi$-periodic function with Fourier series

$$h_1(x)=\frac{2}{\pi}+\frac{4}{\pi} \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{1}{1-4 n^2}\, \cos(2 n x)\right)\tag{8}$$

and the term-wise Fourier transform of formula (8) above is

$$\hat{h}_1(\omega)=\frac{2}{\pi}\, \delta(\omega)+\frac{4}{\pi} \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{1}{1-4 n^2}\, \left(\frac{1}{2}\, \delta\left(\omega+\frac{n}{\pi}\right)+\frac{1}{2}\, \delta\left(\omega-\frac{n}{\pi}\right)\right)\right)\tag{9}$$

which when convolved term-wise with $\hat{g}_1(\omega)$ leads to the series representation

$$\hat{f}(\omega)=-\frac{4}{\pi}\, (\gamma+\log(2 \pi |\omega|))\\+\frac{4}{\pi}\, \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{1}{4 n^2-1}\, \left(2 \gamma-\log\left(\frac{1}{4 \left| n^2-\pi^2 \omega^2\right|}\right)\right)\right)\\=-\frac{4}{\pi}\, \log(\pi |\omega|)+\frac{4}{\pi} \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{\log\left(\left| n^2-\pi^2 \omega^2\right| \right)}{4 n^2-1}\right)\tag{10}.$$

---

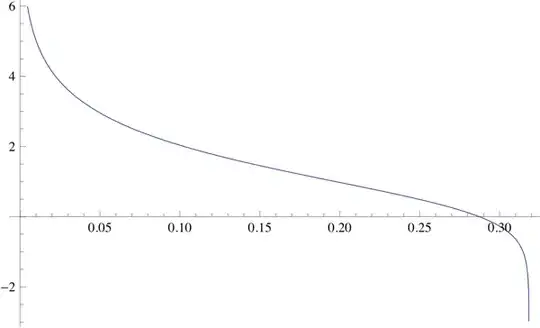
Figure (1) below illustrates formula (10) above for $\hat{f}(\omega)$ evaluated at $N=1000$. Note formula (10) above for $\hat{f}(\omega)$ seems to evaluate consistent with the plots of the Fourier transform in the accepted answer posted by robjohn.

Figure (1): Illustration of formula (10) for $\hat{f}(\omega)$

---

The inverse Fourier transform of formula (10) above leads to the series representation

$$f(x)=\frac{4 (\gamma+\log(2))}{\pi }\, \delta(x)+\frac{2}{\pi |x|}-\frac{4}{\pi |x|} \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{\cos(2 n x)}{4 n^2-1}\right)\tag{11}$$

which interestingly simplifies to the following alternate closed-form representation of $f(x)=|\text{sinc}(x)|$.

$$f(x)=\frac{4 (\gamma+\log (2))}{\pi}\, \delta(x)+\frac{2 i \sin(x) \left(\coth^{-1}\left(e^{i x}\right)-\tanh^{-1}\left(e^{i x}\right)\right)}{\pi | x|}\tag{12}$$

---

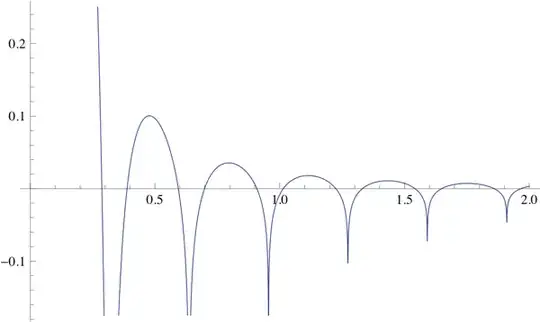
Figure (2) below illustrates the series representation in formula (11) above evaluated at $N=1000$ seems to converge very well to $f(x)=|\text{sinc}(x)|$.

Figure (2): Illustration of series representation in formula (11) for $f(x)=|\text{sinc}(x)|$ in orange overlaid on $|\text{sinc}(x)|$ in blue

---

As was pointed out in the accepted answer posted by robjohn, the function $f(x)=|\text{sinc}(x)|$ can also be evaluated as

$$f(x)=g_2(x)\, h_2(x)\tag{13}$$

where

$$g_2(x)=\text{sinc}(x)\tag{14}$$

and

$$h_2(x)=\text{sgn}(\text{sinc}(x))\tag{15}$$

---

Therefore the Fourier transform

$$\hat{f}(\omega)=\mathcal{F}_x[f(x)](\omega)=\int\limits_{-\infty}^{\infty} f(x)\, e^{-2 \pi i \omega x} \, dx\tag{16}$$

can be evaluated as the convolution

$$[\hat{g}_2(\xi) * \hat{h}_2(\xi)](\omega)=\int\limits_{\infty}^{\infty} \hat{g}_2(\xi)\, \hat{h}_2(\omega-\xi) \, d\xi\tag{17}$$

where

$$\hat{g}_2(\omega)=\mathcal{F}_x[g_2(x)](\omega)=\frac{\pi}{2} (\text{sgn}(1+2 \pi \omega)+\text{sgn}(1-2 \pi \omega))\tag{18}$$

corresponding to a rectangle function of height $\pi$ and width $\frac{1}{\pi}$ is the Fourier transform of $g_2(x)$ and

$$\hat{h}_2(\omega)=\mathcal{F}_x[h_2(x)](\omega)=\frac{\tan\left(\pi^2 \omega\right)}{\pi \omega}\tag{19}$$

is the Fourier transform of $h_2(x)$.

---

The accepted answer posted by robjohn gives a couple of series representations of $\hat{h}_2(\omega)$ the first of which is

$$\hat{h}_2(\omega)=\lim\limits_{K\to\infty} \left(\sum\limits_{k=0}^K (-1)^k\, \frac{\sin\left(2 \pi^2 (k+1) \omega\right)-\sin\left(2 \pi^2 k \omega\right)}{\pi \omega}\right)\tag{20}$$

but the second one should actually be

$$\hat{h}_2(\omega)=\frac{2}{\pi \omega} \lim\limits_{K\to\infty} \left(\sum\limits_{k=0}^K (-1)^k\, \sin\left(2 \pi^2 (k+1) \omega\right)\right)-\delta(\omega)\tag{21}$$

because there's a subtle inconsistency as the inverse Fourier transform of formula (20) above evaluates to $\text{sgn}(\text{sinc}(x))$ whereas the inverse Fourier transform of the series portion of formula (21) above evaluates to $\text{sgn}(\text{sinc}(x))+1$, and consequently formula (21) has been adjusted to include a $-\delta(\omega)$ correction term.

---

Figures (3) and (4) below illustrate formulas (20) and (21) don't converge in the usual sense, i.e. they only converge in a distributional sense in integrals such as their related inverse Fourier transform and convolution integrals.

---

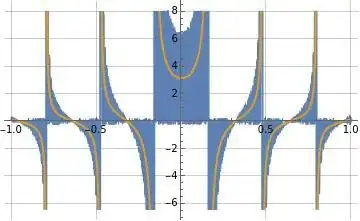
Figure (3): Illustration of formula (20) for $\hat{h}_2(\omega)$ evaluated at $N=1000$ in blue overlaid by the reference function $\hat{h}_2(\omega)=\frac{\tan\left(\pi^2 \omega\right)}{\pi \omega}$ in orange

---

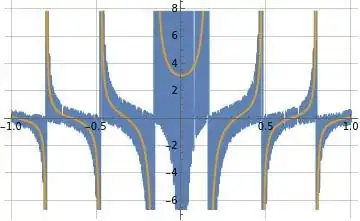
Figure (4): Illustration of formula (21) for $\hat{h}_2(\omega)$ evaluated at $N=1000$ in blue overlaid by the reference function $\hat{h}_2(\omega)=\frac{\tan\left(\pi^2 \omega\right)}{\pi \omega}$ in orange

---

Formulas (20) and (21) above convolved term-wise with $\hat{g}_2(\omega)$ lead to the formulas

$$\hat{f}(\omega)=\lim\limits_{K\to\infty} \left(\sum\limits_{k=0}^K (-1)^k (\text{Si}(\pi (k+1) (2 \pi \omega+1))-\text{Si}(k \pi (2 \pi \omega+1))\\+\text{Si}(\pi (k+1) (1-2 \pi \omega))-\text{Si}(k \pi (1-2 \pi \omega)))\right)\tag{22}$$

and

$$\hat{f}(\omega)=\lim\limits_{K\to\infty} \left(2 \sum\limits_{k=0}^K (-1)^k (\text{Si}(\pi (k+1) (2 \pi \omega+1))+\text{Si}(\pi (k+1) (1-2 \pi \omega)))\right)\\-\hat{g}_2(\omega)\tag{23}$$

for $\hat{f}(\omega)$ where $\hat{g}_2(\omega)$ in formula (23) above corresponds to the rectangle function defined in formula (18) above.

---

Figures (5) and (6) below illustrate formulas (22) and (23) for $\hat{f}(\omega)$ above seem to evaluate similar to formula (10) for $\hat{f}(\omega)$ above (see Figure (1) above), but note formula (23) above illustrated in Figure (6) below doesn't seem to converge as well near $\omega=\pm\frac{1}{2 \pi}$ where the correction term $-\hat{g}_2(\omega)$ takes a step.

---

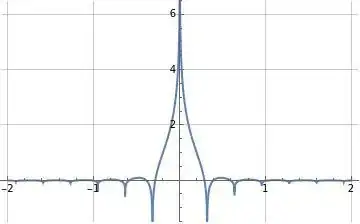
Figure (5): Illustration of formula (22) for $\hat{f}(\omega)$ evaluated at $K=1000$

---

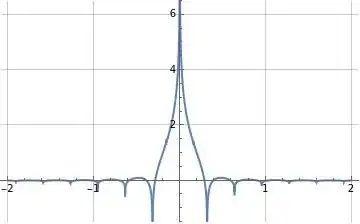
Figure (6): Illustration of formula (23) for $\hat{f}(\omega)$ evaluated at $K=1000$

---

Substituting analytic representations for $\delta(x)$ in formula (21) above and $\hat{g}_2(\omega)$ in formula (23) above leads to

$$\hat{h}_2(\omega)=\frac{2}{\pi \omega} \lim\limits_{K\to\infty} \left(\sum\limits_{k=0}^K (-1)^k\, \sin\left(2 \pi^2 (k+1) \omega\right)\\-\frac{1}{2} \sin\left(2 \pi^2 (K+1) \omega\right)\right)\tag{24}$$

and

$$\hat{f}(\omega)=\lim\limits_{K\to\infty} \left(2 \sum\limits_{k=0}^K (-1)^k (\text{Si}(\pi (k+1) (2 \pi \omega+1))+\text{Si}(\pi (k+1) (1-2 \pi \omega)))\\-\text{Si}(\pi (K+1) (2 \pi \omega+1))+\text{Si}(\pi (K+1) (2 \pi \omega-1))\right)\tag{25}.$$

---

Formula (24) above seems to evaluate more similar to formula (20) illustrated in Figure (3) above than formula (21) illustrated in Figure (4) above.

---

Formula (25) seems to converge near $\omega=\pm\frac{1}{2 \pi}$ more similar to formulas (10) and (22) above than formula (23) above. Figure (7) below illustrates formula (25) above in orange overlaid on formula (23) above in blue where both formulas are evaluated at $N=1000$.

---

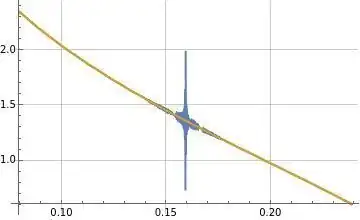
Figure (7): Illustration of formulas (23) and (25) for $\hat{f}(\omega)$ in blue and orange respectively

---

Also I believe the formula

$$\hat{f}(\omega)=\mathcal{F}_x[|\text{sinc}(x)|](\omega)=\frac{2}{\pi} \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{\log\left(\left|\frac{\pi^2 \omega^2-n^2}{\pi^2 \omega^2-(n-1)^2}\right|\right)}{2 n-1}\right)\tag{26}$$

evaluates similar to formulas (10), (22), and (25) above. Formula (26) above was derived from the relationship

$$|\text{sinc}(x)|=\text{sgn}(x)\, \text{sinc}(x)\, r(x)\tag{27}$$

where

$$r(x)=\left\{\begin{array}{cc} 1 & 0\leq x<\pi \\ -1 & \pi \leq x<2 \pi \\ r(x \bmod (2 \pi )) & \text{Otherwise} \\ \end{array}\right.\tag{28}$$

is a $2 \pi$ periodic rectangle wave with Fourier series

$$r(x)=\frac{4}{\pi} \lim\limits_{N\to\infty} \left(\sum\limits_{n=1}^N \frac{\sin((2 n-1) x)}{2 n-1}\right)\tag{29}.$$

---

Answer 4

The more I think about, the more I think that there's no chance of there being a closed form version of the fourier transform of $|\frac{sin x}{x}|$

Look here:

How can you prove that a function has no closed form integral?

If we follow the steps indicated by the answer to this question, we have to say:

$F(\omega) = \int^{+\infty}_{-\infty} f(x) e^{-2i\pi\omega x} dx$ where $f(x) = |\frac{sin x}{x}| $

In order for this integral to have a closed form, we need to find some rational function $h(x)$ which satisfies:

$h'(x) + h(x)g(x) = f(x)$

where $f(x) = |\frac{sin x}{x}| $ and $g(x) = -2i\pi\omega x$

So, if you take $h' + gh = f$ and apply old school integrating factor to it you get the following:

$h(x) = \frac{\int e^{-\pi\omega x^2} |\frac{sin x}{x}| dx}{e^{-\pi\omega x^2}}$

and, between you and me, $h(x)$ does not look like a rational function to me: http://en.wikipedia.org/wiki/Rational_function

I hope I'm wrong because $f(x)$ looks so nice and wavy. It just looks so fourierable to me. It's like, if we can't describe this simple wave as a fourier series without discretizing, then what can we describe as a fourier series?