Angle problem for a trapezoid with two equal sides

Question

Since $AB\parallel DC$, $\angle ACD=\angle CAB=3\alpha.$ By the law of sines in $\triangle ABC$ and $\triangle ACD$, we have $\frac{AB}{\sin5\alpha}=\frac{AC}{\sin(\pi-8\alpha)}$ and $\frac{AD}{\sin3\alpha}=\frac{AC}{\sin(\pi-4\alpha)}.$ Hence, $$\sin3\alpha\sin8\alpha=\sin4\alpha\sin5\alpha$$ and $$\sin5\alpha=2\sin3\alpha\cos4\alpha$$ from which I saw that $\alpha=10^\circ$ is the solution, since $2\sin30^\circ=1$ and $\sin50^\circ=\cos40^\circ.$

I wonder what the the synthetic geometric solution of this problem is. Any ideas?

Answer 1

We are going to "realize" the given figure as a subset of diagonals of an 18-gon (see Fig. 1).

Consider a unit radius circle with center $O$ and diameter $A'E'$, and its regular inscribed polygon with 18 vertices, $A'$, $E'$ being being opposite vertices. See fig. 1 for the definition of different points we will need in the sequel.

We will rely in a permanent way on the inscribed angle theorem, without mentionning it (in fact, almost all angles in Fig. 1 are multiples of $\beta:=20°$).

Let us define $D'$ as the intersection of line $I'B'$ and line $G'C'$.

Triangle $OC'I'$ being isoceles ($OC'=0I'$) with angle $\hat{C'OI'}=60°$ is equilateral. Triangle $OB'C'$ is equilateral as well ; as a consequence, $I'OB'C'$ is a lozenge with a center called $J'$. Therefore as the diagonals of a lozenge are orthogonal, $I'D'C'$ is the altitude of triangle $OC'I'$ ; in particular, $D'$ also belongs to line $A'E'$.

Lines $G'C', H'F'$ and $A'B'$, having a common perpendicular bissector (red line in fig. 1), these line segments are parallel. Therefore :

$$A'B' \ // \ D'C' \tag{1}$$

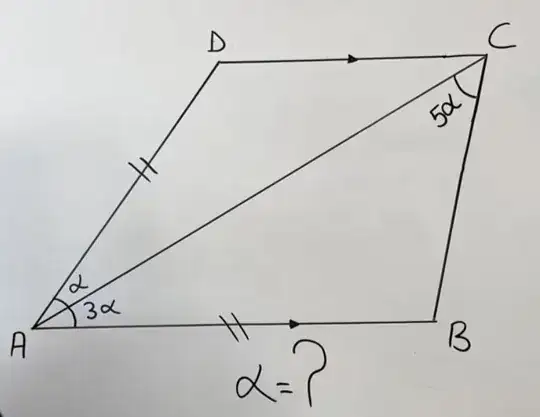
We can now map "isometrically" trapezoid $A'B'C'D'$ onto trapezoid $ABCD$. Indeed, corresponding angles are in the same ratio 1:3:5. Therefore, angle $\alpha$ is half of angle $\beta$, i.e. $10°$.

Geogebra picture :

Fig. 1 : A fascinating figure with a lot of properties...

---

Edit 1: Following your remark, as we know that $A'B' \ // \ D'C'$ (see (1) above) the trapezoid property is verified ; it remains to show that triangle $B'A'D'$ is isosceles.

As inscribed angle $\hat{I'B'A'}$ is equal to $70°$, and due to the fact that angle $\hat{B'A'D'}$ is equal to $40°$, the third angle in triangle $B'A'D'$ has value $180°-70°-40°=70°$ proving that this triangle is isosceles, as desired.

---

Edit 2: Let us consider point $J$ (center of lozenge). As $\tfrac12 = OJ = OD' \cos 20°$, we have $OD'=\frac{1}{2 \cos 20°}$. Besides, $A'B'=2 \sin 50°=2 \cos 40°=2(2 (cos 20°)^2 -1)$.

Relationship $A'B'=A'D'$ gives rise to the non-trivial relationship :

$$2(2 (cos 20°)^2 -1)=1+\frac{1}{2 \cos 20°}$$

otherwise said : $x=\cos 20°$ is a root of the third degree equation :

$$2(2x^2-1)=1+\frac{1}{2x}\tag{2}$$

a property that we have been able to establish geometrically.

By comparison, a classical method for obtaining equation (2) is by using Chebyshev polynomials (of the first kind) in the following way :

$$T_3(\underbrace{\cos 20°}_x)=\cos(3 \times 20°)=\tfrac12$$

$$4x^3-3x=\tfrac12$$

which is identical to relationship (2).

Answer 2

In the figure, $F$ is a point on $BA$ such that $\angle ACF=\alpha$.

We are done if we can show that $\Delta FCD$ is an equilateral triangle.

By angle chasing,

$$\angle BFC=\angle BCF=2 \alpha$$ $$\angle EBC=\angle BEC=4 \alpha$$ Together with $$\angle FAC= \angle FCA = \alpha,$$

we have

$$BF=BC=CE \tag {1}$$ $$CF=AF \tag{2}$$ $$AB=AD=DE \tag{3}$$

$(1)$ to $(3)$ implies that $$\begin{aligned} CF &= AF \\ &= AB-BF \\ &= DE-CE\\ &= CD \end{aligned}\tag{4}$$

$\because \beta=\delta=\gamma$ and $BF=BC$, we have $\Delta BDF \cong \Delta BDC$ and hence $$CD=DF \tag{5}$$

$(4)$ and $(5)$ implies that $\Delta FCD$ is equilateral.

Hence $$6\alpha=60^{\text o}$$ $$\alpha=10^{\text o}$$