4

In the figure, $A$ is the midpoint of a side of a regular 18-gon. The black polygon is a regular Nonagon. $O$ is the centre. I found that $BC, EF,OA$ are always concurrent but I couldn’t prove it. Any hint or solution will be appreciated. I tried adding lines and construct some triangles but seem non of them work.

I am good at plane euclidean geometry, trigonometry (Up to Year 12)but I suspect there is a elegant euclidean geometrical proof existing.

1

brainjam
  • 9,172
Mat
  • 151
  • 5
    Can three truths also be concurrent? – Oscar Lanzi Feb 06 '23 at 00:57
  • The nonagon seems to be irrelevant to the question as all points of interest are defined by the $18$-gon anyway. – heropup Feb 06 '23 at 01:06
  • @heropup Oh yeah, I have it there because i was originally playing around with the Nonagon, and then just constructed the 18 gon and discovered this fact. – Mat Feb 06 '23 at 01:37
  • Assume they are not. Just assign the angles and you will see it. Almost every single angle in that drawing is known. – quantinho Feb 06 '23 at 09:31
  • @quantinho No, it wont work as the angle doesnt implies concurrent – Mat Feb 06 '23 at 11:09
  • 1
    FYI: Considering the figure embedded in a $36$-gon, we see that all three lines correspond to chords. ($OA$ is, in particular, part of a diameter.) Tests of concurrence are given by formulas in this answer of mine. In particular, using $(1)$ there, your situation corresponds to $$(a_0,a_1;b_0,b_1;c_0,c_1)=(0,18; 1,25;5,33)$$ (where the vertex closest to your $A$ has index $0$, $F$ has index $1$, etc). – Blue Feb 08 '23 at 15:58

2 Answers2

2

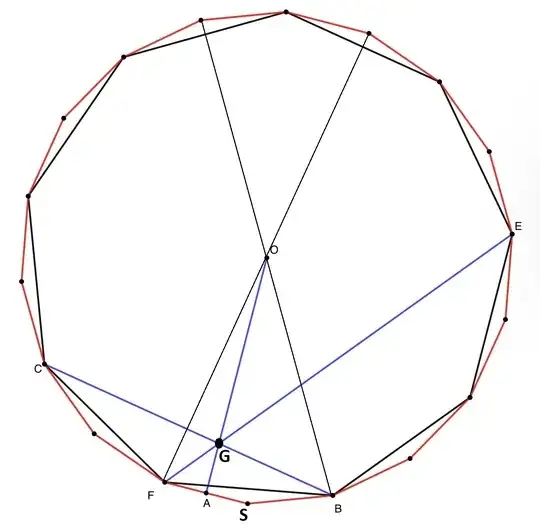
Instead of proving that those three are concurrent, we prove that $OG$ bisects $FS$ (at the point $A$).

Note that $O$ is the circumcenter of the $18-$gon.

Let's assume $\angle FOA =x$.

We have:

$$1=\frac {OG}{FG} \times\frac {BG}{OG} \times \frac {FG}{BG} \\ =\frac {\sin \angle OFG}{\sin x} \times \frac{\sin \angle GOB}{ \sin \angle OBC} \times \frac{\sin \angle CBF}{\sin \angle GFB} \\ = \frac{ \sin 30^{\circ}}{\sin x} \times \frac{\sin (40^{\circ} -x)}{\sin 50^{\circ}} \times \frac{\sin 20^{\circ}}{\sin 40^{\circ}} \\ \implies \frac{\sin (40^{\circ} -x)}{\sin x}=\frac { 2\sin 50^{\circ} \sin 40^{\circ}}{\sin 20^{\circ}} \\ =\frac{\cos 10^{\circ}}{\sin 20^{\circ}} \\ \implies \frac{\sin (40^{\circ} -x)}{\sin x}= \frac{\frac{1}{2}}{\sin 10^{\circ}}=\frac{\sin (40^{\circ} -10^{\circ})}{\sin 10^{\circ}} \\ \implies x=10^{\circ}.$$

On the other hand, $\triangle FOS$ is an isosceles triangle, and $\angle FOS =20^{\circ}.$ Hence, we are done.

enter image description here

Reza Rajaei
  • 6,236
1

Let $D$ be the reflection of $C$ over $OH$, so that $BC$, $FD$, and $OH$ concur at some point $X$ (by symmetry over $OH$). Let $G, H$ be the reflections of $E, F$ over $OA$. Then $\triangle CEG$ and $\triangle XFH$ have parallel corresponding sides, so they are homothetic about some point $Y$, which lies on $BC$, $EF$, $GH$, and also $OA$ (by symmetry over $OA$). ∎

diagram

Anders Kaseorg
  • 9,972
  • [+1] Nice! Problems like this - 3 concurrent diagonals of a regular polygon (36-gon here) - are typically solved using trig bashing. I wonder whether your technique can be used in general for this sort of problem. – brainjam Feb 18 '23 at 00:23