Geometry - A variant of Langley's Adventitious Angles

Question

I've stumbled upon a variant of Langley's Adventitious Angles problem (also known as The World's Hardest Easy Geometry Problem), see figure. Usually, this problem is solved by constructing a set of equilateral triangles. But the usual solution does not apply directly to this case. Any help would be appreciated. Thanks!

Given

1. angle $ECB$ = angle $DCE$ = $22.5$ degrees
2. angle $EBC$ = $112.5$ degrees
3. angle $ABE$ = $33.75$ degrees
4. angle $CDE$ = $22.5$ degrees

The objective is to find $y$ and $z$.

My work so far

So far I have computed all angles except $y$ and $z$, by exploiting the fact that the angles in a triangle sum to $180$ degrees. Additionally, I've noted that the lengths of $DE$ and $CE$ are equal.

Answer 1

Focus on the triangle $BCD$. Note that $CA$ is the internal angle bisector of $BCD$. Moreover, $BA$ is the external angle bisector of $DBC$. This means that $A$ is the $C$-excenter of the triangle $BCD$. Thus $$\angle DAC = \dfrac 12 \angle DBC = \dfrac 12 \cdot 112.5^\circ = 56.25^\circ.$$ Since $A$ is the $C$-excenter of $BCD$, $DA$ is the external angle bisector of $\angle CDB$. Thus $$\angle BDA = 90^\circ - \dfrac 12 \angle CDB = 90^\circ - \dfrac 12 \cdot 22.5^\circ = 78.75^\circ.$$

Answer 2

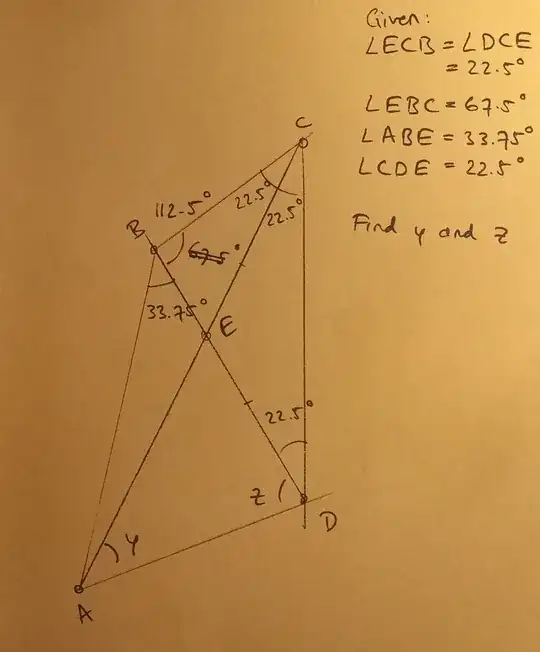
"Adventitious angles" issues can be solved by many different techniques ; see these very didactic pages.

My preference go to the "incarnation" of the given figure in a net of diagonals of some regular $n$-gon ; here we will take $n=16$ because all angles are multiples of $11.25$ degrees = $360/(2 \times 16)$ degrees. See Fig. 1 below.

The solution steps are as follows :

1. First install some points of the figure, here $A,C,D$ (and also $C',D'$ which will be used later on) as vertices of a suitable $n$-gon, here with $n=16$ as can be seen on Fig. 1. In this way, applying the inscribed angle property ; conditions (1) and (4) in your question are fulfilled.

2. Then define the remaining point $B$ as the intersection $B:=C'D \cap CD'$ and check that conditions (2) and (3) are fulfilled as well. This can be done by elementary analytic geometry calculations and/or by using symmetry properties with respect to lines $AF$ or $II'$ (please note that the diameter line defined by midpoints $I,I'$ contains point $F$ and, of course, the center $O$ of the $16$-gon).

3. Once this checking has been done, finding the values of angles $Y,Z$ is almost immediate by considering the arcs they sustain ($5 \times 11.25°$ for $Y$, $7 \times 11.25°$ for $Z$).

For more details about such a method, please see my recent answer to a similar problem here .

Fig. 1 : The given quadrilateral inscribed in a cobweb of diagonals of a 16-gon ("hexadecagon"). Drawing made with Geogebra.