Envelope of lines giving a conic section

Question

This problem originates from another question, which was closed for lack of context. I found a solution but some details are still missing, as explained below.

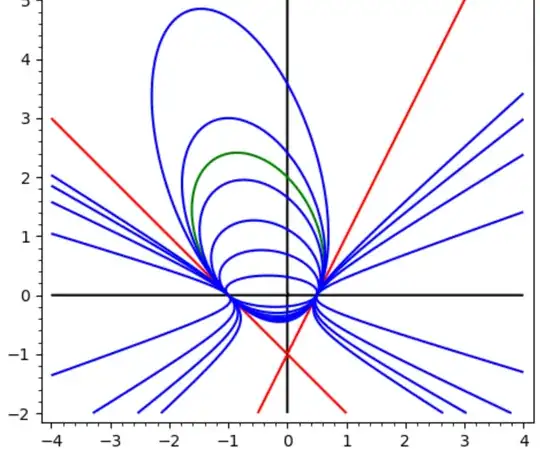
Given an angle and a point $P$ inside it, consider all chords $$ such that $\angle =90°$. Show that the envelope of those chords is a conic section.

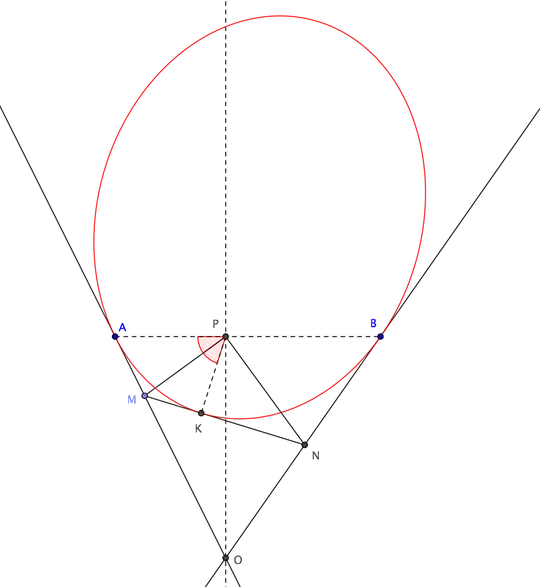
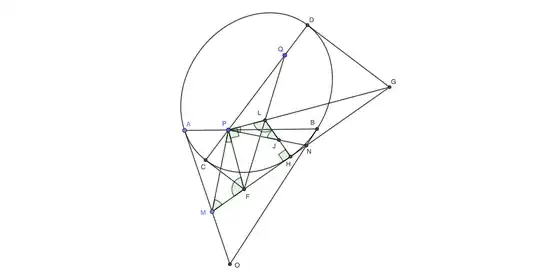
Let $A$, $B$ be the intersections of the sides with the perpendicular to $OP$ at $P$, where $O$ is the vertex of the angle (see figure below) and consider points $M$, $N$ on $OA$, $OB$ such that $\angle MPN=90°$.

Suppose I managed to show that the tangency point $K$ between line $MN$ and the envelope is such that $\angle MPK=\angle APM$. If so we immediately get that the envelope is a conic, tangent to the given lines at $A$, $B$ and having $P$ as focus. This follows from a nice theorem (see here for a proof):

If two tangents are drawn to a conic from an external point, then they subtend equal angles at the focus.

Note that the conic is uniquely defined from its tangencies at $A$, $B$ and its focus at $P$. Moreover, point $O$ lies on the directrix relative to focus $P$ and the type of conic section depends on $\angle AOB$:

• it is an ellipse if $\angle AOB<90°$;

• it is a parabola if $\angle AOB=90°$;

• it is a hyperbola if $\angle AOB>90°$.

EDIT.

From the above theorem we obtain as a corollary that:

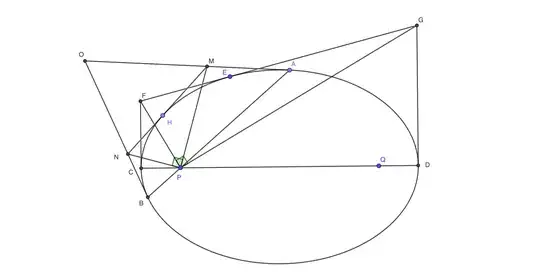
If from the endpoints of a focal chord $APB$ tangents $OA$, $OB$ are drawn, and a third tangent at $K$ cuts $OA$, $OB$ at $M$ and $N$ respectively, then $\angle MPN=90°$.

Proof: we have $\angle APM=\angle MPK$ and $\angle KPN=\angle NPB$, hence:

$$ \angle MPN=\angle MPK+\angle KPN= {1\over2}(\angle APK+\angle KPB)={1\over2}\cdot 180°. $$

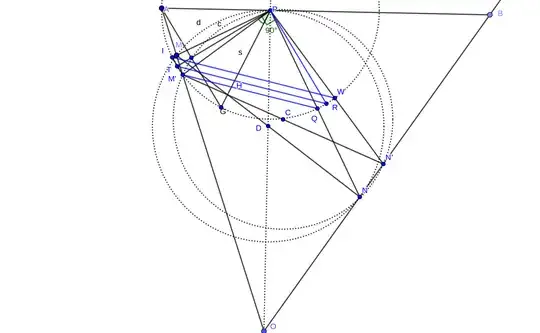
As observed by Edward Porcella in his answer, the desired property is just the converse of this corollary and can be proved by RAA: construct the unique conic section with focus $P$ and tangents $OA$, $OB$, then consider a chord $$ of $\angle AOB$ such that $\angle =90°$. If $MN$ were not tangent to the ellipse we could construct a tangent $M'N'$ to the ellipse, parallel to $MN$. But then $\angle MPN=90°=\angle M'PN'$, which is impossible.

This neat proof is simpler and doesn't require proving $\angle MPK=\angle APM$. Nevertheless, I'd like to find a simple proof of the property shown below.

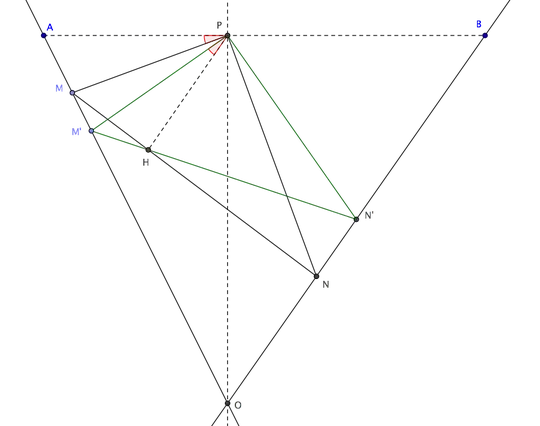
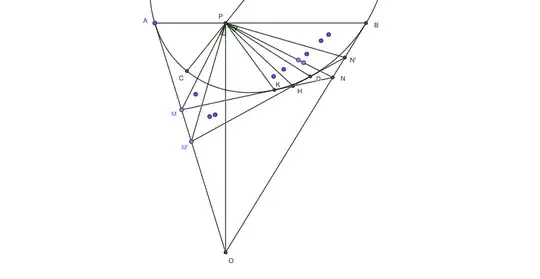
Consider a second chord $M'N'$ of $\angle AOB$, such that $\angle M'PN'=90°$, intersecting $MN$ at $H$ (see figure below). Tangency point $K$ is then the limiting position of $H$ as $M'\to M$.

Experimenting with GeoGebra, I found that $\angle M'PH=\angle APM$ for any position of $M'$. If so, in the limit $M'\to M$ we have $\angle M'PH\to \angle MPK=\angle APM$ as it was to be proved. But I cannot prove that $\angle M'PH=\angle APM$: it should be an easy geometric result, but it somehow eludes me. How to show that?

Answer 1

This is an entirely different route than the OP is following in proving the statement (requires analytic geometry), but it may provide some insight for the geometric proof. Choose the coordinates of point $P:(0,0)$; arbitrary coordinates can always be restored later. Then, define the lines emanating from $O$

$$O_1: y=a_1x+b_1\\O_2: y=a_2x+b_2 $$

and a pair of orthogonal lines emanating from $P$ $$P_1:y=\lambda x,~~ P_2: y=-\frac{x}{\lambda},~~~\lambda\geq 0$$

We name the intersection points of these lines $M_{1}:P_1\times O_1,~ N_1:P_1\times O_2,~ M_2:P_2\times O_1,~ N_{2}:P_2\times O_2$

$$M_1:\left(\frac{b_1}{\lambda-a_1}, \frac{\lambda b_1 }{\lambda-a_1}\right),~~ N_1:\left(\frac{b_2}{\lambda-a_2}, \frac{\lambda b_2 }{\lambda-a_2}\right)\\ M_2\left(-\frac{\lambda b_1}{\lambda a_1+1}, \frac{ b_1 }{\lambda a_1+1}\right),~~ N_2:\left(-\frac{\lambda b_2}{\lambda a_2+1}, \frac {b_2 }{\lambda a_2+1}\right)$$

There are two possible segments that can be formed. However, they both belong to the same geometric locus since $\vec{M_1N_2}(a_1,b_1,a_2,b_2)=-\vec{M_2N_1}(a_2,b_2,a_1,b_1)$; exchanging the labels of the lines $O_1, O_2$ does not affect the geometry of the problem. We will focus on the choice $M_1N_2$.

The final step is to calculate the envelope of the chords $M_1N_2$; after some algebra, it becomes evident that the each segment labeled by $\lambda$ can be described by the equation

$$(X,Y)\in M_1N_2:X(a_2b_1\lambda^2+\lambda(b_1-b_2)+a_1b_2)+Y(-\lambda^2b_2+(a_1b_2-a_2b_1)\lambda-b_1)=-(\lambda^2+1)b_1b_2$$

If the points $(X,Y)$ belong to the envelope, it must be true that the derivative of the above equation with respect to $\lambda$ also holds true:

$$X(2a_2b_1\lambda+(b_1-b_2))+Y(-2\lambda b_2+(a_1b_2-a_2b_1))=-2\lambda b_1b_2$$

Upon eliminating $\lambda$, it follows that the envelope satisfies the quadratic form

$$((b_1-b_2)X+(a_1b_2-a_2b_1)Y)^2=4(a_2b_1X-b_2 Y+b_1b_2)(a_1b_2X-b_1 Y+b_1b_2)$$

and therefore describes a conic section.

To analyze the type of conic we obtain, we must compute the discriminant, which can be factored as

$$D=4b_1b_2(a_1a_2+1)[(a_1b_2-a_2b_1)^2+(b_1-b_2)^2]$$

The sign of the discriminant is controlled by the quantity $b_1b_2(a_1a_2+1)$, which is positive if and only if $P$ is inside the acute angle formed by the lines $O_1,O_2$. To prove this, first define vectors that generate the two lines, $v_{1,2}=(1,a_{1,2})$. Note that $$\vec{OP}=\frac{b_2}{a_2-a_1}v_1-\frac{b_1}{a_2-a_1}v_2:=c_1v_1+c_2v_2$$ The sign of the components of $v_1,v_2$ determines which vectors the point $P$ lies between. If for example $c_1>0, c_2>0$, it lies between $v_1$,$ v_2$ and if $c_1>0, c_2<0$ it lies between $v_1, -v_2$. Lastly, note that $$a_1a_2+1=\cos\hat{(v_1,v_2)}\sqrt{(1+a_1^2)(1+a_2^2)}$$ which means that

$$\text{sgn}(D)=-\text{sgn}(c_1c_2\cos\hat{(v_1,v_2)})$$

which proves that when $P$ is inside the acute angle, the resulting conic is an ellipse, and when outside it's a hyperbola. The only way to obtain a parabola is to make $O_1, O_2$ orthogonal.

Answer 2

Here is a simple analytical solution (having many common features with the solution by @K. Grammatikos) .

Let us take WLOG a system of coordinates such that

• $P$ is the origin of the axes,

• Lines $L_M$ and $L_N$ intersect in $O=(-1,0)$ and have slopes $-m<0$ for $L_M$ and $n>0$ for $L_N$, i.e., with resp. equations

$$(PM) : y=-mx-1 \ \ \ \text{and} \ \ \ (PN) : y=nx-1, \tag{1}$$

• Orthogonal lines $PM$ and $PN$ have resp. equations $$(L_M) : y=sx \ \ \ \text{and} \ \ \ (L_N) : y=-\frac{1}{s}x.\tag{2}$$

Parameter "s" is the moving parameter (whereas $m$ and $n$ are fixed).

Fig. 1 : Sides $L_M$ and $L_N$ of the "angle" are featured in red. Line segments $MN$ are blue.

Using (1) and (2), it isn't difficult to obtain the following coordinates for points $M$ and $N$ :

$$M=\left(\frac{-1}{s+m}, \ \ \frac{-s}{s+m}\right) \ \ \ N=\left(\frac{s}{sn+1}, \ \ \frac{-1}{sn+1}\right) $$

as homographical functions of parameter $s$ (sometimes also called "Möbius functions").

Therefore (see here), the equation of straight line $MN$ is given by :

$$\begin{vmatrix}\frac{-1}{s+m}&\frac{s}{sn+1}&x\\\frac{-s}{s+m}&\frac{-1}{sn+1}&y\\1&1&1\end{vmatrix}=0$$

which is equivalent to :

$$\begin{vmatrix}-1&s&x\\-s&-1&y\\s+m&sn+1&1\end{vmatrix}=0$$

The expansion of this determinant as a quadratic polynomial is $s$ :

$$s^2\underbrace{(y-nx+1)}_P+s\underbrace{(m+n)y}_Q+\underbrace{(mx+y+1)}_R=0\tag{3}$$

allows to apply a result given in this question If a family of straight lines is $\lambda^2 P+\lambda Q+R=0$ ,then the family of lines will be tangent to the curve $Q^2=4PR.$

with its (validated) proof given by @Blue. It expresses the fact that the discriminant of (3) is equal to $0$ :

$$Q^2-4PR=0 \tag{5}$$

$$((m+n)y)^2-4(y-nx+1)(mx+y+1)=0\tag{6}$$

which is indeed the equation of a conic curve, an ellipse in general, for example in the case $m=1$ and $n=2$ represented as a green curve on Fig. 2. $\square$

Important remark : We can recognize in $P=0$ and $R=0$ the resp. equations of $L_M$ and $L_N$ ! It isn't odd when you refer to the theory of pencils of conics : indeed (5) belongs to the pencil of conics given by

$$Q^2+\mu PR=0, \ \ \mu \ \text{being any nonzero value}\tag{7}$$

which is a linear combination of two degenerate conic curves ; see Fig. 2 ($Q^2=0$ represents a double line and $PR=0$ represents a pair of lines) : in fact, (7) describes any conic curve tangent to lines $P=0$ and $R=0$ at the intersection points with double line given by $Q^2=0$.

Fig. 2 : (particular case $m=1$ and $n=2$) Some curves belonging to the pencil of conics given by (7) for different values of $k$ ; some are ellipses, others are hyperbolas . Solution curve (6) is featured in green : it is an ellipse. $Q=0$ is the $x$-axis, $P=0$ and $R=0$ are featured in red like on Fig. 1.

Answer 3

I. In Conics III, 45, where the points now known as foci make their first appearance, Apollonius shows that if two tangents at the end of the axis of a conic section intersect a third tangent, then the lines from a focus to the intersection points are perpendicular to each other. Thus in the ellipse below, with foci $P$, $Q$, and tangents $CF$, $DG$ perpendicular to the major axis, he proves $\angle GPF=90^o$.

This appears to be a special case of a more general truth, which he does not prove:

If any chord in a conic section passes through a focus, and tangents at the chord’s endpoints intersect a third tangent, then lines joining the points of intersection to the focus make a right angle.

Thus in the figure, where tangents at $A$ and $B$ intersect the tangent through $H$ at $M$, $N$,$$\angle MPN=90^o$$In the posted question, we are given a point $P$ within a given $\angle BOA$, with $A$ and $B$ chosen such that $OP\perp AB$, and seek proof that all segments $MN$ subtending a right angle $MPN$ are tangents to a conic section having focus $P$, tangents $OA$, $OB$, and point $O$ lying on the directrix. (In the case proven by Apollonius, $CF$ and $DG$ do not meet, i.e. point $O$ is infinitely remote).

II. If Apollonius’ theorem does apply more generally, i.e. when a tangent intersects tangents not from the major axis but from any chord passing through one focus, then it seems the question is asking for proof of the converse:

If a point $P$ lies within an angle $BOA$, and $OP$ is perpendicular to $AB$, then every segment $MN$ joining $OA$, $OB$ as base of a right triangle with vertex $P$ is tangent to a conic section having focus $P$ and tangents $OA$, $OB$.

III. Had Apollonius proven III, 45 more generally, proof of its converse—by reductio ad absurdum?—might not be too difficult. For what it's worth, I give below my progress so far at extending the proof of Apollonius, although proof of its converse seems to be the ultimate goal here.

In the next figure $HL$ joins tangent $MN$'s point of contact with the intersection of $PG$, $FQ$.

Thus, by Conics III, 45 & 47$$\angle FPL=\angle LHF=90^o$$making $PLHF$ a cyclic quadrilateral, $\angle PLH$ supplemental to $\angle HFP$, so that$$\angle PLJ=\angle PFM$$One more pair of equal angles is needed, to prove $\triangle PLJ\sim \triangle PFM$, making $\angle MPF=\angle JPL$, and hence$$\angle MPN=\angle FPG=90^o$$

Addendum: Using the theorem referenced in his post, OP's edit completes my attempt to prove the generalized version of Apollonius Conics III, 45, and shows how its converse ("Given an angle and a point inside it, consider all chords such that ∠=90°. Show that the envelope of those chords is a conic section.") easily follows.

If we may assume a conic section, then, with focus $P$, tangents $OA$, $OB$, right angles $MPN$, $M'PN'$, with $MN$, $M'N'$ tangent at $K$, $D$, and intersecting at $H$, and want to prove$$\angle M'PH=\angle APM$$we can start with their complements $\angle HPN'$ and $\angle MPO$.

Since $\angle MPN=\angle M'PN'=90^o$, then $\angle MPM'=\angle NPN'$.

And since $\angle M'PN'=\angle OPB=90^o$, then $\angle M'PO=\angle N'PB$. Therefore$$\angle MPO=\angle NPB$$

Since $NB$, $NK$ are tangents, then$$\angle NPB=\angle KPN$$And since $HD$, $HK$ are tangents, then $\angle HPD=\angle KPH$.

And since $\angle KPH=\frac{1}{2}\angle KPD$, and $\angle DPN’=\frac{1}{2}\angle DPB$, then$$\angle HPN’=\frac{1}{2}(\angle KPD+\angle DPB)=\frac{1}{2}\angle KPB=\angle KPN$$ so that$$\angle HPN’=\angle KPN=\angle NPB=\angle MPO$$Therefore, the complements of the first and last,$$\angle M’PH=\angle APM$$

Answer 4

In the picture we have:

$PM\bot PN$

$PM'\bot PN'$

Therefore:

$\angle MPM'=\angle WPQ$

$AT$ is bisectors of angle $MPM'$ and $PT\bot PR$, so $PR$ is the bisector of angle WPQ. I is intersection of PM with circle d , So we have:

$TR||IW||M'Q$

So T is the mid point of arc $IM'$ that means $PT\bot IM'$ . Also:

$ PT\bot AG\Rightarrow AG||IM'$

Which results in:

$Arc AI=Arc M'G\Rightarrow \widehat{APM}=\widehat{M'PH}$