Why is the past uniquely determined by the present in classical mechanics and ODE?

Question

I just began reading Ordinary Differential Equations by Arnol'd, and in the first few paragraphs of the first chapter, Arnol'd says the following:

The theory of ordinary differential equations is one of the basic tools of mathematical science. This theory makes it possible to study all evolutionary processes that possess the properties of determinacy, finite-dimensionality, and differentiability.... A process is called deterministic if its entire future course and its entire past are uniquely determined by its state at the present time.... Thus, for example, classical mechanics considers the motion of systems whose future and past are uniquely determined by the initial positions and initial velocities of all points of the system.

I suspect that I'm misinterpreting this statement, because it seems entirely false to me that the past is uniquely determined by the present in classical mechanics. Are there not distinct states which evolve (under the laws of mechanics) into the same final state after some time?

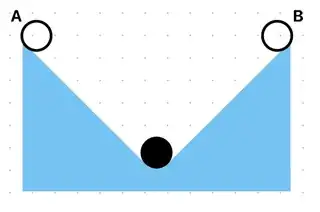
As a silly toy example, imagine that we record the state of a ball with four coordinates: its position in the 2D plane $(x,y)$, as well as its velocity vector $(\dot x,\dot y)$. Let's say the ball starts at the top of a ravine with no initial velocity (depicted below). Regardless of whether the ball starts in position A or position B at initial time $t_0$, we can model the evolution of the ball at all times $t\geq t_0$, allowing us to associate one state with every value of $t\in[t_0,\infty)$. That is, the future of the ball is uniquely determined by the present, as Arnol'd states. Crucially, however, the ball ends up in the same final state whether the initial state is in position A or position B. Hence, imagine that we first observe the ball at rest at the bottom of the ravine, so that time $t_0$ corresponds to the black ball in the picture below. There is no way to determine whether ball's past lies in state A or state B, so we cannot uniquely determine the ball's past based on its present state in this scenario.

This is just the first example that comes to mind, but surely there are endless other examples in classical mechanics where there are multiple distinct $t_{0}$ states that evolve into the same $t_{f}$ state, no? Wouldn't this mean that observing the $t_{f}$ state as the "present" moment prevents us from uniquely determining the state of the system at $t_0$? What am I misinterpreting about Arnol'd's statement?

Answer 1

There are two points that you should address.

1. the state of a mechanical system is given by position and velocity together. Two balls in the same position can move differently if they have different velocity

2. in the example you give you are dealing with friction. If you imagine there is no friction, the two balls will never stop at the bottom and will always have a different state. On the other hand if you take into account friction you should track the position of all the atoms of the blue funnel which will have different evolutions in the two scenarios

Answer 2

You are interpreting the statement correctly. Assuming perfect knowledge, classical mechanics should allow you to perfectly predict the past given the present. Abstractly, this is because time evolution is governed by a Hamiltonian vector field on phase space, which (maybe under mild assumptions necessary to rule out examples like Norton's dome) has a flow which is a diffeomorphism for all time - a smooth map on phase space with smooth inverse.

Moreover, classical mechanics has time reversal symmetry; this means that, again assuming perfect knowledge, in classical mechanics, if you believe the future is determined by the present, then the past must also be determined by the present ("just" reverse the velocities of all particles).

In your scenario with the ravine, when you imagine that the ball eventually stops at the bottom regardless of where it started, you are imagining

1. that friction will eventually dissipate the ball's kinetic energy, and
2. that there is no meaningful information in the heat released by friction.

Both of these are true in practical terms due to statistical mechanics, the uncertainty principle, etc. etc. However, in terms of the mathematical formalization of classical mechanics this is not correct. The simplest modification is to remove friction as Emanuele discusses.

We could also discuss an enormously more complicated model of the situation in which we explicitly model the effect of friction in terms of the Avogadro's number of particles that make up the surface of your slopes, and of the balls. Microscopically friction involves electromagnetic interactions between these particles, and when the ball moves past a given section of slope it jostles the particles on that slope (as well as jostling the air, etc). This jostling is what is happening microscopically when friction dissipates kinetic energy and produces heat. So assuming perfect knowledge, in classical mechanics this jostling contains enough information to recover the past of the ball.

Answer 3

That example with the ball is not Hamiltonian. It is an oversimplification that loses the conservation of energy. Indeed, at the start the ball loses some potential energy, which converts into kinetic energy. But then the kinetic energy suddenly disappears at the bottom. If this model were exact, we would be violating the principle of conservation of energy.

A more precise model would account for the vibration of the atoms at the bottom of the ravine. Then, the two final states would be very different.

Answer 4

Classical mechanics traditionally lies in Lipschitz-kind of ODEs, which stands uniqueness of solutions, but they are just a model, since as example, they cannot accurately represent any phenomena which stops moving in finite time: their solutions are power series which cannot become a constant value after some point or it would violate the Identity Theorem.

But this doesn't mean you cannot make more complicated models for increasing accuracy, as example you could use non-Lipschitz kind of ODEs like this question where a real life example is cited and could be answered as mentioned in the question with a piecewise solution that achieve rest in finite time, which keeps uniqueness only among the initial conditions and when the system stops moving, but after uniqueness is broken, you do could fall in issues like the presented by the Norton's Dome example and here when you cannot determine the system behavior from the initial conditions, here is not math which is going to tell you what it would happen in reality, but instead, the physics of how models are fitting or not the experimental results.

Math, technically speaking have nothing to do with reality, is reality consistency which makes math a magic tool to model and predict outcomes. Math is more like the art of making logic statements derived from some axioms (in my own words), axioms that don't have to emulate necessarily our reality at all (think of some intricate non-Euclidean geometries or dual numbers as examples), this is why math don't follow the traditional scientific method. Now, why reality shows to be such it could be accurately model with math falls into the metaphysics of science, and out of the scope of the question (but as engineer, we are very lucky it is like it is).

As a toy example of what I mean, think of the classic electromagnetic wave equation in one spatial dimension: $v_{tt}=c^2v_{xx}$, from this kind of equation special relativity was derived as you could see in this YT video, but it does not imply I cannot built solutions to the mentioned wave equation that will violate relativity like in this question: every model has assumptions and limitations (like the wave equation in this example), and reality just is what it is, is not solving equations to behave as it does (so far I know).

Answer 5

This is a bit of a circular argument.

It's not true to say that classical mechanics and ODEs mean that the past is uniquely determined by the present in all cases.

It's only the case when the state of the present is sufficiently specified in such a way that the past is uniquely determined... which is, of course, where the circularity comes in.

Consider a simple harmonic oscillator.

We know that finding its velocity and position require integration. We also know that integration introduces constants that can only be resolved by applying boundary conditions.

So, generally, and ODE with insufficient boundary conditions cannot uniquely determine the past.