1

On the maximum rate of change of solutions to the wave equation, Could it be limited?

Intro_________

In the classic 1D Wave Equation $u_{tt}-c^2u_{xx}=0$ with a traveling wave solution $f(x-ct)$, their speed it is always described in literature by the Group velocity $v_g$ and the Phase velocity $v_p$, being the group velocity the one describing the information speed, and the phase velocity the speed at which the wave travels in the medium, $v_p =c$ in this case - here are equivalent since the phase is $\varphi=x-ct \Rightarrow v_p=v_g$ (correct me if I am mistaken please).

If I see the animation in Wikipedia for a modulated example where the mentioned speeds are different, you can see the group velocity in a green dot, and the phase velocity in a red dot: Wikipedia image example

But if I focus my attention only on a stripe of the picture, I can see there is another speed that is not mentioned, that is the vertical speed at which a particle of the blue string would be moving up and down as the wave pass through it, as you could see in the cropped slide, this vertical speed could be much faster than the previous two velocities mentioned:

Section of the Wikipedia image

In the abstract sense of a wave, I understand the change of its value could have no physical sense, but if I am describing a string like a guitar chord, this additional vertical speed $v_y$ will have a physical meaning of spatial position, and this should be limited also by the relativistic limit.

But as I reviewed in this question, I could make solutions to the wave equation where the vertical speed is unbounded (its what I believe, at least, $\partial f/\partial \varphi$ it is unbounded), so in this example should exists non-zero time intervals where the chord particles are going to vertically move faster than the speed of light, this without violating nothing on the wave equation since its speed $c$ has nothing to do with the speed at which their particles vibrates in the vertical direction (this is my interpretation of being a solution to the wave equation):

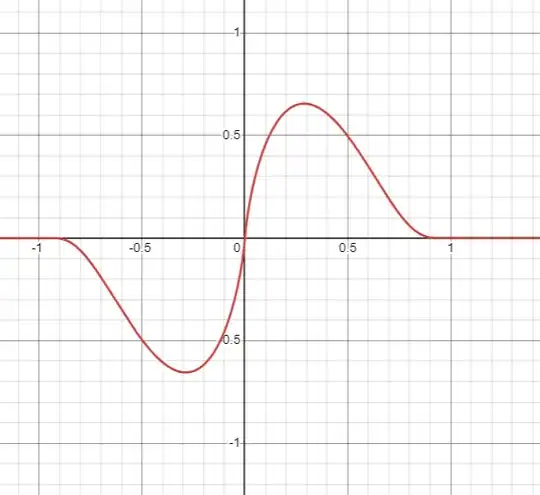
$$f(\varphi) = \begin{cases} 0,\quad \varphi=0 \\ 0, \quad |\varphi|\geq 1\\ \varphi\ln(\varphi^2)\ \exp\left(\dfrac{\varphi^2}{\varphi^2-1}\right),\,\text{otherwise}\end{cases}$$

You could see its plot assuming $\varphi=x-ct$ with $c=1$ and $x=0$:

Make up example

Question_______

  1. What is the formal name of this vertical speed $v_y$?
  2. It described correctly by $v_y:=\dfrac{\partial f}{\partial t}\equiv \dfrac{\partial f}{\partial \varphi}\dfrac{\partial \varphi}{\partial t} = -c \dfrac{\partial f}{\partial \varphi} $? If not, Which is its proper formulation? Here one could see that the vertical speed is proportional to the term $\partial f/\partial \varphi$ which goes unbounded in the extreme case example.
  3. How the solutions of the wave equation would be restricted if I limit this vertical speed $v_y$ such it always $v_y < c$? (or $v_y \leq c$ if makes better physical meaning)... It is possible to force this restriction on the 1D wave equation $u_{tt}-c^2u_{xx}=0$? Or another more complicated wave equation is required? Which formula have then this restricted wave equation?
  4. Any references for this vertical speed $v_y$ are very welcome! Extension for higher dimensional wave equations too.

Obs: this question was modified after the comment by @EricTowers

PS: I know beforehand that a physicist will chose a solution $f(\varphi)$ such it fulfill physical limits, which is why I am not interested as much on the physics behind, but instead, in finding a mathematical tool for modeling the problem more accurately from the very beginning: find a differential equation where the restriction is forced within it by its own formulation.

Motivation

After watching this video about how electromagnetic fields fails Galilean Transformations, which leads to the Lorentz Transform and the discover of Special Relativity, it looks really weird to me that the same framework of EM equations which leads to the relativistic limit for speed $v\leq c$, also leads to make the classic wave equation for light which equation could allow the existence of waves that can violate the relativistic limit, as shown in the mentioned example from above, is like the model has a hidden mathematical inconsistency since the same equations leads to contradictory behaviors.

Joako
  • 1,957
  • Worth pointing out that the derivation of the wave equation requires "small displacements" from the equilibrium position. Reading the first two or three pages here might help. Real, physical strings with non-small displacements (i.e., non-small slopes) don't satisfy the wave equation. Large displacements also produce longitudinal stress, so the points of the string are no longer constrained to their "cropped slides". – Eric Towers Oct 05 '24 at 05:45
  • Not-small-amplitude also quickly reaches beyond solvability. See the Answer at https://physics.stackexchange.com/questions/78924/work-done-by-vibrating-string-without-small-amplitude-assumption for examples of how little "reality" one has to add to the vibrating string model to get differential equational models that are too gnarly to teach to students. – Eric Towers Oct 05 '24 at 06:09
  • @EricTowers Thanks for the link. There, in Eq. 41 a vertical speed $v_y$ is defined as $$v_y:=\dfrac{\partial f}{\partial t}\equiv \dfrac{\partial f}{\partial \varphi}\dfrac{\partial \varphi}{\partial t}=-c\dfrac{\partial f(\varphi)}{\partial \varphi}$$ meaning I have mistaken the formula in the question, and also that in the example the vertical speed is really unbounded. So my doubts are valid, but I don't found in the text of the link restrictions for limiting $v_y$ in mi first fast read. – Joako Oct 05 '24 at 06:18
  • "If $\mathrm{d}\psi$ is small (more precisely if the slope $\mathrm{d}\psi/\mathrm{d}x$ is small; see below), then we can make the approximation that all points in the string move only in the transverse direction." – Eric Towers Oct 05 '24 at 06:21
  • @EricTowers sorry but I don't get your point: I am trying to figure out (or applying) the speed limit exactly in the transverse direction, where the points are allowed to move. In this video, it would be the speed at which any stick tip is moving up or down. – Joako Oct 05 '24 at 06:29
  • The wave equation is derived under the assumption that the angles are small (corresponding to small displacements). Your example function has undefined slope at $\varphi = 0$, so the wave equation does not apply. So what equation do you propose to replace it with? Several of your specific questions (and some of the no longer applicable foundational information) require a choice of governing equation. – Eric Towers Oct 05 '24 at 06:35
  • @EricTowers that is not true if you think on the electromagnetic wave equation. The fact is that it is used successfully to model almost every wave phenomena, and I wonder "why?" if is not fulfilling the relativistic speed limit, and what would happen if you force that restriction on it. The equation is just $$\frac{\partial^2 f}{\partial \varphi^2} = \frac{\partial^2 f}{\partial \varphi^2}$$ being expanded from the spatial coordinate in the right hand side, and on the temporal coordinate on the left hand side. The limitatioms you mention are just the excuses to fit spring systems to it. – Joako Oct 05 '24 at 15:34
  • "The limitatioms you mention are just the excuses to fit spring systems to it." is exactly backwards. The spring system that match strings in tension are the correct model (with nonlinear spring tensions to match real, physical objects). Even the electromagnetic field deviates from the wave equation at large amplitude (at energies where particle-antiparticle production is possible -- q.v. pair-instability supernova). – Eric Towers Oct 05 '24 at 16:23
  • @EricTowers in that sense nothing fulfills the wave equation: my question is focus in the description and how it would change if a limit its vertical speed (this is why I ask in a math and not physics forum)... for seen it fail in the EM wave you just need a green laser pointer and a glass vase with olive oil: through the oil the green laser will trace a red light path, frequency changes aren't possible on a linear differential equation – Joako Oct 05 '24 at 18:16

1 Answers1

-1

The speed of sound is vastly lower than the speed of light. The highest sound speed I could find is diamond at 12000 m/sec, which is 1/25000 the speed of light. The 1D wave equation you quote is a good approximation for small amplitudes. Probably the first two things it ignores are the added energy contained in curvature of the string and the second order added length as the amplitude grows. Either of these will make the equation inaccurate long before the transverse velocities become relativistic. In the case of longitudinal sound waves the amplitude cannot get so high that atoms in the crystal notice the neighboring ones for electrostatic reasons instead of chemical bonding reasons as we consider each atom to be connected to its equilibrium position by linear springs.

This is a case of "All models are wrong, but some are useful." The simple equation is a model which is reasonably accurate within a useful range of conditions. The transverse velocity is well below the speed of light throughout this range of conditions.

Ross Millikan
  • 383,099
  • thanks for the answer but you missed the point. I am not asking about the physics, but instead about how I could change the model in order to improve its accuracy. I am interested in the math point of view of how the wave equation works, and how it would change if I introduce a bound to the rate of change of $\partial f/\partial t$ – Joako Oct 08 '24 at 05:31
  • You would have to more accurately model the change in energy with the transverse displacement. Currently it is just considered a linear spring, so the added energy is quadratic in the transverse displacement and the spring constant is given by the tension in the string. This fails at large displacements. I don't know what better relationship there is. – Ross Millikan Oct 08 '24 at 14:26
  • I don't know neither, but thinking in springs, at least for the harmonic scenarios, for high amplitudes there are closed form solution through Jacobi's elliptic functions – Joako Oct 13 '24 at 02:13
  • 1
    I am not familiar with those solutions, but am sure they only incorporate a (few) specific deviations from linearity. The usual expression for springs is $E=\frac 12kx^2$ where $x$ is the displacement from equilibrium and $k$ is the (small amplitude) spring constant. They probably add a term in $x^3$ or $x^4$ and find the solutions you mention. For high amplitudes like you are interested in other things can happen, like the spring breaking. Before it breaks you can have terms in so many orders that this expansion is not useful. – Ross Millikan Oct 13 '24 at 02:32