I'm studying this article and I've understood most of it precisely, but I can't figure out one crucial passage at page 4.
They have the Laplace transform $\tilde{Q}(z)$ of the real function $Q(x)$ in the form $$\tilde{Q}(z)\sim z^{v-2}exp\biggl(z+\frac{\delta^2x}{4z}\biggr)$$ and they want to apply the inversion formula for the Laplace transform to get the starting function $$Q(x) \sim \int_C\frac{\tilde{Q}(z)}{2\pi i}dz$$
Little note: I'm not sure I truly understand how they can use this formula with a generic contour $C$ instead of the classic vertical line. If you want to help me on this I asked this question alone here.
Then they start applying this formula to different contours:
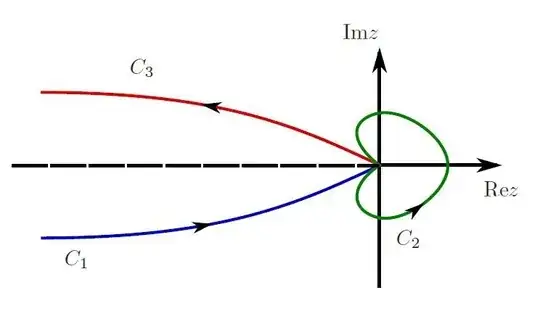
they claim: "Putting everything together and choosing the Hankel contour $C = C_1 \cup C_2 \cup C_3$ our first solution reads $$Q_1(x)\sim e^{-z_0x}x^{(1-v)/2} \quad \times\\ \qquad \qquad \qquad \qquad \times \qquad \Bigl(\frac{u}{2}\Bigr)^{1-v}\int_C\frac{1}{2\pi i}\frac{e^{z+u^2/(4z)}}{z^{2-v}}dz$$ with $u=\delta\sqrt{x}$. In the last line we recognize the contour integral representation of the modified Bessel function of the first kind $I_\nu(u)$ with order $\nu = 1 − v$."
Again I'm not really sure how $C = C_1 \cup C_2 \cup C_3$ can be treated as the Hankel contour but, more importantly, I don't understand how to get to the modified Bessel function of the first kind from that expression. Fortunately I found this question, which fits perfectly if I'm not mistaken.
The problem is when they use another contour and they claim: "take $C = C_1 \cup(−C_3)$, we find $$Q_2(x)\sim e^{-z_0x}x^{(1-v)/2} \quad \times\\ \qquad \qquad \qquad \qquad \qquad \qquad \times \qquad \biggl(-\frac{\pi}{2sin(\pi\nu)}\biggr)\Bigl(\frac{u}{2}\Bigr)^{1-v}\int_C\frac{1}{2\pi i}\frac{e^{z+u^2/(4z)}}{z^{2-v}}dz$$ In the last line we recognize the contour integral representation of the modified Bessel function of the second kind $K_\nu (u).$"
Again I don't understand how to get to the modified Bessel function of the second kind from that expression and this time I haven't found anything helpfull.
I'm pretty lost at this point so any help would be much appreciated.