I'm studying this article and I've understood most of it precisely, but I can't truly understand one thing about the formula for the Inverse Laplace transform they use.
I know the traditional definition of inverse Laplace transform, which is the Fourier-Mellin's integral $$Q(x)=\mathcal{L}^{-1}\{\tilde{Q}(z)\}=\frac{1}{2\pi i}\lim_{T\rightarrow\infty}\int_{\gamma-iT}^{\gamma+iT}e^{zx}\tilde{Q}(z)dz$$ but they claim $$Q(x) \sim \frac{1}{2\pi i} \int_C\tilde{Q}(z)dz$$ with $C$ a generic path as long as
(i) it runs in the domain of analyticity of $\tilde{Q}(z)$,
(ii) $\tilde{Q}(z)$ has the same (finite) values at the two endpoints.
I don't really understand how one can formally state that this formulas are equivalent. My guess is that they are using a residue argument and Cauchy's theorem, but I would appreciate if someone can explain this a little bit better and formally.
To give you more insight on my confusion my case is with this Laplace transform
$$\tilde{Q}(z)\sim z^{v-2}exp\biggl(z+\frac{\delta^2x}{4z}\biggr)$$
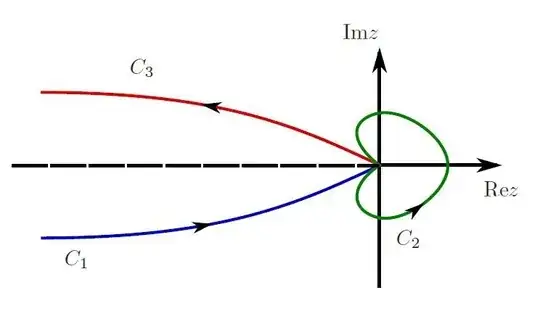
so they state "Since there might be a branch cut along the negative real axis the contour cannot cross that. One can also see that the endpoints have to go either to infinity or zero in the $Re(z) < 0$ half plane because only then, due to the exponential function, will the values vanish at both ends." and then they present the following contours: