How to construct the segment $p=\sqrt{ab}$ given the segments $a$ and $b$?

Question

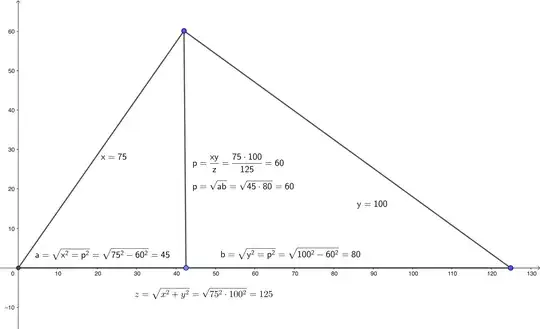
Given the segments $a$ and $b$, how to construct the segment $p=\sqrt{ab}$

This question is from geometry textbook. At the back of the book, there is a hint to solve the problem but anyways the hint didn't help me. I couldn't understand the hint itself. Here is the hint they gave:

First construct the segment $c=\frac{a+b}{2}$ and the segment $d=\frac{|a-b|}{2}$. Then the segment that you are trying to find will be equal to $x=\sqrt{c^2-d^2}$.

As this question is from the Pythagorean theorem topic, I thought it is somehow related to $c^2=a^2+b^2$, but I couldn't make any connections.
Can you please help me understand the hint they gave and the problem itself?

Answer 1

Usually I see construction of $\sqrt{ab}$ using Geometric mean theorem and Thales' circle - which seems (to me) as the most straightforward approach.

But the approach suggested in the hint is perfectly fine. You have $$\left(\frac{a+b}2\right)^2-\left(\frac{a-b}2\right)^2=ab,$$ i.e., you want a right triangle with hypotenuse $c=\frac{a+b}2$ and one of the legs $d=\frac{|a-b|}2$.

So you can simply take a segment of the length $c$, create a Thales' circle. Then you take a circle from one of the endpoints with the radius $d$. For the right triangle that you get, the other leg has length $\sqrt{c^2-d^2}$.

See also: Compass-and-straightedge construction of the square root of a given line? and some of the questions linked there.

Answer 2

This is indeed a relationship found among parts of a Pythagorean triple. It relates a perpendicular $\,(p)\,$ line segment between the hypotenuse and the right angle to the resulting smaller line segments of the hypotenuse. Here is the smallest triple I know of in which all of this question's elements are integers.

You can see from the formulas at the bottom that $\,a\,$ and $\,b\,$ are derived from the Pythagorean Theorem where $\,p\,$ is just a leg of the smaller triangles dividing the big one.