2

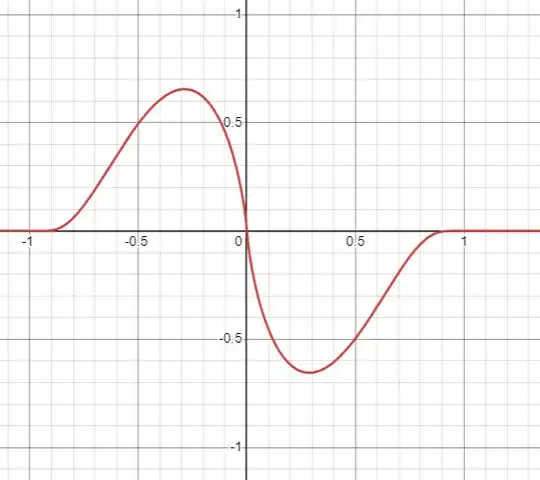
I am trying to understand when solutions of the wave equation could have issues, so I made a continuous function which some extreme behaviors: has compact-support given by a smooth bump function term, and also has issues in a zero-measure point where it becomes somehow "smoothly"/"softly" into a non-differentiable function.

Since the 1D wave equation $f_{xx}=\dfrac{1}{c^2}f_{tt}$ could indeed stand some distributions as solutions (at least as is said vaguely in Wikipedia), I want to know if the following function could be a solution of the 1D wave equation, and if not, if there is some ways it could make sense (like in weak solutions): for $z = x - ct$, the function I made is: $$f(z) = \begin{cases} 0,\quad z=0 \\ 0, \quad |z|\geq 1\\ z\ln(z^2)\ \exp\left(\dfrac{z^2}{z^2-1}\right),\,\text{otherwise}\end{cases}$$

From its plot it looks quite innocent and similar to a common wave (plot at $t=0$):

plot at t=0

But just in the simple scenario of $t=0$ their derivatives blown-up, so I got lost in trying to figure out if it could fulfill the 1D wave equation or not. Hope you could explain why is a so (if it fulfill it or not).

But if it do solves the solution, hope you could comment what is happening near $z=0$, since my intuition tells me that near that point the wave-points would be moving faster than the wave speed $c$: Would that violate causality? or at least the restrictions the same wave equation is supposedly fulfilling? or the wave speed don't restrict at all the speed the wave-points could have?

Joako
  • 1,957

1 Answers1

1

For any smooth function $f=f(z)$, letting $$ u(t,x):= f(x-ct)$$ defines a solution to the 1d wave equation you wrote. Indeed, $$ \partial^2_t u(t, x)=c^2f''(x-ct), $$ and $$ \partial^2_x u(t, x)=f''(x-ct), $$ so $\partial^2_t u = c^2\partial^2_x u$. This computation carries through to the distributional setting. So that function you have indeed is a solution to the wave equation and it does not exhibit any special phenomena. Its graph will be a translate in time of the graph you showed. Any singularity in the $x$ derivative will just translate away along the light cone $x=ct$.

Giuseppe Negro
  • 34,508
  • 1
    Thanks for the answer. Wolfram-Alpha says something similar. – Joako Sep 26 '24 at 22:31
  • What I don't understand is, thinking in $y\equiv f(z)$ as another spatial variable, near $z=0$ the points in the wave are "almost teleporting" from $y>0$ to $y<0$, which can be seen since $f_t(z)$ has points where got undefined... Does this mean that "c" only determine the speed of the wave in the x-axis? so the movement in y-axis is not constraint? if that is the case, kind of in projectiles where x-axis speed is independen of y-axis speed, it is weird also since nothing stop the wave from "detached" the points.. It is possible to have discontinous solutions then? – Joako Sep 26 '24 at 22:35
  • 1
    "possible to have discontinous solutions then?" Absolutely. Did you know this nice applet? https://phet.colorado.edu/sims/html/wave-on-a-string/latest/wave-on-a-string_all.html I regularly spend time playing with it. Try setting damping to 0, putting on manual mode, and giving it a sudden jerk upward with your mouse. That is essentially a discontinuous solution, with a jump discontinuity that travels along the $x$ axis. – Giuseppe Negro Sep 27 '24 at 15:11
  • Nice link... is easy to see that vertical speed has nothing to do with the wave speed.... I guess in real life the wave would behave as wave so far the particle links don't tear appart.... Do you know some modified version of the wave eqn which take into account this issue? (don't know if it would be just a discontinuity on how much stress the link could stantd or instead a restriction on maximum vertical speed)... I am courious because somehow in 2D waves the restriction somehow happens naturally: higher frequency beams are more directional than low frequency (more spherical) – Joako Sep 27 '24 at 15:46
  • 1
    I don't really know, but you are touching upon deep properties of the higher-dimension wave equation compared with the 1d wave equation. In 1d, the wave equation is very simple, there is even a general formula for solutions: https://en.wikipedia.org/wiki/D%27Alembert%27s_formula All of this disappears in 2d, 3d and beyond. Much more complicated. – Giuseppe Negro Sep 27 '24 at 18:17
  • thanks for your answers... the link was quite revealing. I would try now to make somehow a 2D smooth version of a singular solution like the one of the question to see what happens (but I am not sure even from where to start) – Joako Sep 27 '24 at 20:15