Questions on integrating $\int_0^{\infty} \frac{x^{\frac{1}{3}}}{1 + x^2} dx$ using contour integrals

Question

We have the following integral to solve $$ I = \int_0^{\infty} \frac{x^{\frac{1}{3}}}{1 + x^2} dx $$ I've managed to solve this integral. Using the substitution $u = x^2$ we can show that $I = \frac{1}{2}B(\frac{2}{3}, \frac{1}{3})$, where $B$ is the Beta-function. We use the Gamma representation of the Beta-function, and, finally, Euler's reflection formula to show that $I = \frac{\pi}{\sqrt{3}}$.

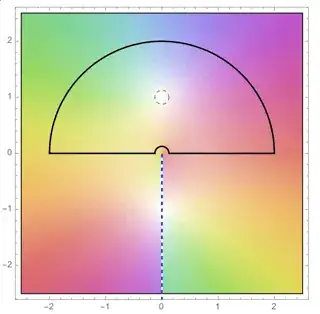
Now I want to try to solve the same integral using contour integration. As contour we take the upper half circle $\Gamma_R$ with radius $R > 1$. We have one pole at $i$ within the upper half circle $\Gamma_R$. Using the residue theorem we find on the one hand (we write $z$ instead of $x$, as the problem becomes complex) $$ \oint_{\Gamma_R} \frac{z^{\frac{1}{3}}}{1 + z^2} dz = \oint_{\Gamma_R} \frac{z^{\frac{1}{3}}}{(z - i)(z + i)} dz = i 2 \pi \frac{i^{\frac{1}{3}}}{i2} = \pi i^{\frac{1}{3}}. $$ On the other hand $$ \oint_{\Gamma_R} \frac{z^{\frac{1}{3}}}{1 + z^2} dz = \int_{-R}^{R} \frac{z^{\frac{1}{3}}}{1 + z^2} dz + \int_{0}^{\pi} \frac{R^{\frac{1}{3}} e^{i \frac{\theta}{3}}}{1 + R^2 e^{i2\theta}} iRe^{i\theta} d\theta. $$ Letting $R \to \infty$, the second integral goes to zero because the denominator dominates the nominator. We have $$ \pi i^{\frac{1}{3}} = \int_{-\infty}^{\infty} \frac{z^{\frac{1}{3}}}{1 + z^2} dz = \int_{-\infty}^{0} \frac{z^{\frac{1}{3}}}{1 + z^2} dz + \int_0^{\infty} \frac{z^{\frac{1}{3}}}{1 + z^2} dz = \int_{0}^{\infty} \frac{(-u)^{\frac{1}{3}}}{1 + u^2} du + I, $$ where we used the substitution $u = -z$ in the first integral, and observed that the second integral is our target integral $I$. We can write $i = e^{i\frac{\pi}{2}}$ so that $i^{\frac{1}{3}} = e^{i\frac{\pi}{6}} = \frac{\sqrt{3}}{2} + i \frac{1}{2}$. As $u$ is non-negative, we can write $(-u)^{\frac{1}{3}} = (e^{i\pi} u)^{\frac{1}{3}} = e^{i\frac{\pi}{3}} u^{\frac{1}{3}} = (\frac{1}{2} + i\frac{\sqrt{3}}{2}) u^{\frac{1}{3}}$. Plugging in these equalities in the equation above gives $$ \pi \frac{\sqrt{3}}{2} + i \frac{\pi}{2} = \int_0^{\infty} \frac{(\frac{1}{2} + i\frac{\sqrt{3}}{2}) u^{\frac{1}{3}}}{1 + u^2}du + I = \frac{3}{2} I + i \frac{\sqrt{3}}{2} I. $$ Taking either the real or imaginary part of this equation gives the target integral $I = \frac{\pi}{\sqrt{3}}$.

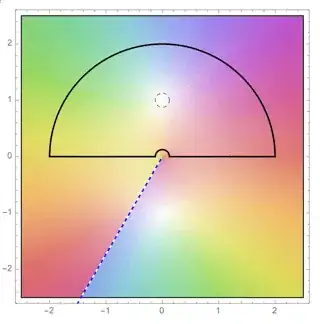
So far, so good. But here is my question. There are multiple cube roots possible. Two other solutions for $i^{\frac{1}{3}}$ are $-i$ and $-\frac{\sqrt{3}}{2} + i \frac{1}{2}$, two other solutions for $(-1)^{\frac{1}{3}}$ are $-1$ and $\frac{1}{2} - i \frac{\sqrt{3}}{2}$. If I use any of the other cube roots in the method above, I won't get the solution $I = \frac{\pi}{\sqrt{3}}$. For one of them I even get that something non-zero is equal to zero.

1. Why do the other cube roots not work for this method?
2. How do I know, beforehand, which cube root to take? How does this work in general for any $z^{\frac{1}{n}}$, where $n > 2$?

Thank you in advance!

Answer 1

$\newcommand{\bbx}[1]{\,\bbox[15px,border:1px groove navy]{\displaystyle{#1}}\,} \newcommand{\braces}[1]{\left\lbrace\,{#1}\,\right\rbrace} \newcommand{\bracks}[1]{\left\lbrack\,{#1}\,\right\rbrack} \newcommand{\dd}{\mathrm{d}} \newcommand{\ds}[1]{{\displaystyle #1}} \newcommand{\expo}[1]{\,\mathrm{e}^{#1}\,} \newcommand{\ic}{\mathrm{i}} \newcommand{\on}[1]{\operatorname{#1}} \newcommand{\pars}[1]{\left(\,{#1}\,\right)} \newcommand{\partiald}[3][]{\frac{\partial^{#1} #2}{\partial #3^{#1}}} \newcommand{\root}[2][]{\,\sqrt[#1]{\,{#2}\,}\,} \newcommand{\sr}[2]{\,\,\,\stackrel{{#1}}{{#2}}\,\,\,} \newcommand{\totald}[3][]{\frac{\mathrm{d}^{#1} #2}{\mathrm{d} #3^{#1}}} \newcommand{\verts}[1]{\left\vert\,{#1}\,\right\vert}$ Lets consider $\ds{\oint_{\mathscr{C}}{z^{1/3} \over 1 + z^{2}}{\dd z \over 2\pi\ic} = {\pars{\expo{\pi\ic/2}}^{1/3} \over 2\ic} + {\pars{\expo{-\pi\ic/2}}^{1/3} \over -2\ic} = \sin\pars{\pi \over 6} = \color{red}{\large{1 \over 2}}}$.

$\ds{\mathscr{C}}$ is a contour which "takes care" of the $\ds{z^{1/3}}$ $\ds{\underline{principal}\ branch\mbox{-}cut}$. Namely, $\ds{z^{1/3} = \verts{z}^{1/3}\expo{\ic\on{arg}\pars{z}/3}\ }$ where $\ds{-\pi < \on{arg}\pars{z} < \pi\ \wedge\ z \not= 0}$. Note that there are two poles inside such contour: $\ds{\expo{\pm\pi\ic/2}}$. Contributions to the whole integration vanish out along the big arc of radius $\ds{R\ \pars{\sr{{\rm as}\ R\ \to\ \infty}{\propto}1/R^{2/3}}}$ and along the indent -of radius $\ds{\epsilon}$-around $\ds{0\ \pars{\sr{{\rm as}\ \epsilon\ \to\ 0^{+}}{\propto} \epsilon ^{2/3}}}$

Therefore, the whole integration is reduced to be along paths above and below the $\ds{z^{1/3}\ \mbox{branch-cut}}$. \begin{align} & \color{#44f}{\oint_{\mathscr{C}}{z^{1/3} \over 1 + z^{2}}{\dd z \over 2\pi\ic}} = \int_{-\infty}^{0}{\pars{-x}^{1/3}\expo{\pi\ic/3} \over 1 + x^{2}}{\dd x \over 2\pi\ic} + \int_{0}^{-\infty}{\pars{-x}^{1/3}\expo{-\pi\ic/3} \over 1 + x^{2}}{\dd x \over 2\pi\ic} \\[5mm] = & \expo{\pi\ic/3}\int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}{\dd x \over 2\pi\ic} - \expo{-\pi\ic/3}\int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}{\dd x \over 2\pi\ic} \\[5mm] = & \ {2\ic\sin\pars{\pi/3} \over 2\pi\ic} \int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}\dd x = \color{red}{\large{\root{3} \over 2\pi}\int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}} \dd x} \end{align} Therefore, -see the above $\ds{\color{red}{red}}$ expressions-, $$ {1 \over 2} = {\root{3} \over 2\pi} \int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}\dd x \\ \implies \int_{0}^{\infty}{x^{1/3} \over 1 + x^{2}}\dd x = {\pi \over \root{3}} = \bbx{\color{#44f}{\Large{\root{3} \over 3}\,\pi}} \approx 1.8138 $$

Answer 2

Judging by your description, you are integrating $$f(z) = \frac{z^{1/3}}{1+z^2} = \frac{\lvert z\rvert^{1/3} e^{i \tfrac13 \arg z}}{1+z^2}$$ along the positively-oriented contour pictured below:

Like you say, there are several possible cube roots, hence the need for restricting yourself to a specific branch. I've done just that in the plot; by cutting the plane along the negative imaginary axis, we are confined to

$$\arg z\in\left(-\dfrac\pi2,\dfrac{3\pi}2\right) \implies \frac13 \arg z \in\left(-\dfrac\pi6,\dfrac\pi2\right)$$

(More generally, the interval $\arg z\in\left(-\dfrac\pi2+2n\pi,\dfrac{3\pi}2+2n\pi\right)$, but choosing $n=0$ is simplest). This ensures $\arg z$ takes on exactly one value for any $z$ not lying on the cut.

On this particular branch, we have e.g. $\arg(-1)=\pi$ and $\arg i=\dfrac\pi2$. However, $\arg(-i)$ -- really any $\arg(ix)$ where $x<0$ -- is undefined, since it approaches $-\dfrac\pi2$ from the right of the cut, and $\dfrac{3\pi}2$ from the left. Hence $(-1)^{1/3}=e^{i\pi/3}$ and $i^{1/3}=e^{i\pi/6}$, while in order to secure a concrete value of $(-i)^{1/3}$, we must decide which of $-\dfrac\pi2$ or $\dfrac{3\pi}2$ to include in the domain of $\arg z$.

On the other hand, if we had picked $n=1$ so that we're on the branch with $\arg z\in\left(\dfrac{3\pi}2,\dfrac{7\pi}2\right)$, we would instead have $-1=e^{i\color{red}3\pi}\implies (-1)^{1/3}=e^{i\pi}=-1$ and $i=e^{i\color{red}5\pi/2}\implies i^{1/3}=e^{i5\pi/6}$, and $(-i)^{1/3}$ remains ambiguous.

On yet another hand, consider a branch where the cut is made along any ray from the origin and pointing into the half-plane $\Im z<0$. (Pictured with the cut rotated by $\pi/6$ rad from the negative imag. axis)

Now we have $\arg z\in\left(-\dfrac\pi3,\dfrac{5\pi}3\right)$, so that e.g. $(-1)^{1/3}=e^{i\pi/3}$, $i^{1/3}=e^{i\pi/6}$, but this time we definitively have $-i=e^{i3\pi/2}\implies (-i)^{1/3}=e^{i\pi/2}=i$, at the cost of making $z^{1/3}$ ambiguous for all $z$ on this cut.

---

Let's evaluate the integral on the first branch. The residue at the enclosed pole is

$$\underset{z=i=e^{i\pi/2}}{\operatorname{Res}} f(z) = \lim_{z\to i} \frac{\lvert z\rvert^{1/3} e^{i\tfrac13 \arg z}}{z+i} = \frac{e^{i\tfrac13\cdot\tfrac\pi2}}{2i} = \frac12 e^{-i\pi/3}$$

so that by the res. theorem (and omitting details re. the circular arcs), as expected,

$$\begin{align*} i2\pi \sum \operatorname{Res} &= \oint_C f(z) \, dz \\ \pi e^{i\pi/6} &= \int_{-\infty}^0 \frac{|x|^{1/3} e^{i \tfrac13 \cdot \pi}}{1+x^2} \, dx + \int_0^\infty \frac{|x|^{1/3} e^{i\tfrac13\cdot0}}{1+x^2} \, dx \\ &= \left(1+e^{i\pi/3}\right) \int_0^\infty \frac{x^{1/3}}{1+x^2} \, dx \\ \implies I &= \pi \frac{e^{i\pi/6}}{1+e^{i\pi/3}} = \frac\pi{\sqrt3} \end{align*}$$

We get the same result on the second branch, where $\arg z\in\left(\dfrac{3\pi}2,\dfrac{7\pi}2\right)$:

$$\begin{align*} \underset{z=i=e^{i\color{red}5\pi/2}}{\operatorname{Res}} f(z) &= \frac{e^{i\tfrac13 \cdot\tfrac{5\pi}2}}{2i} = \frac12 e^{i\pi/3} \\ \stackrel{\text{res.thm.}}\implies \pi e^{i5\pi/6} &= \int_{-\infty}^0 \frac{\lvert x\rvert^{1/3} e^{i \tfrac13 \cdot 3\pi}}{1+x^2} \, dx + \int_0^\infty \frac{\lvert x\rvert^{1/3} e^{i \tfrac13 \cdot 2\pi}}{1+x^2} \, dx \\ \implies I &= \pi \frac{e^{i5\pi/6}}{-1 + e^{i2\pi/3}} = \frac\pi{\sqrt3} \end{align*}$$

I encourage OP to work out the details using the third aforementioned branch and verify that $I$ ends up the same value.

---

Now, to explicitly (and hopefully) answer your questions:

1. The "other cube roots" don't work because their cubes don't belong to the branch we chose. For example, $$-1=e^{i(\pi+2n\pi)} \in \left\{\ldots,e^{-i3\pi},e^{-i\pi},e^{i\pi},e^{i3\pi},e^{i5\pi},\ldots\right\}$$ but only $-1=e^{i\pi}$ is found on the first branch.

2. The choice in branch dictates the value of $\arg z$ wherever it appears. You control $\arg z$ and by extension $\dfrac13\arg z$. The general case is no different. (See e.g. here, where it's demonstrated that $x^{1/2}$ and $x^{1/4}$ get essentially the same treatment.)

---

Lastly, I'd like to suggest an alternate approach. Eliminating the root by substituting in the integral $x\to x^3$ allows us to circumvent consideration of branch cuts altogether:

$$I = \int_0^\infty \frac{x^{1/3}}{1+x^2} \, dx = \int_0^\infty \frac{3x^3}{1+x^6} \, dx$$

This can be evaluated by integrating along the boundary of a circular sector. (It should be clear why a semicircle won't work.) See this similar example.