I was trying to solve this problem from Dan.
What I did:
Firstly, I used $2tan^{-1}(p)$ as the mapping function to map a point $p$ on the real line to unit circle. This should map [$-\infty,\infty$] to [$-\pi,\pi$] on the circle. The chord length (for radius=$1$) is $2sin\left(\frac{arc\ length}{2}\right)$.
If I choose 3 points on the real line as $(-x,0),(0,0)$ and $(y,0)$, (where $x$ and $y$ are positive numbers) with the mid point to map to an arbitrary $0$ position on the circle, the chord lengths for the 3 sides forming a triangle (let's call them side1, side2 and side3) are $\frac{2x}{\sqrt{x^2+1}}$, $\frac{2y}{\sqrt{y^2+1}}$ and $\frac{2(x+y)}{\sqrt{x^2+1} \sqrt{y^2+1}}$.
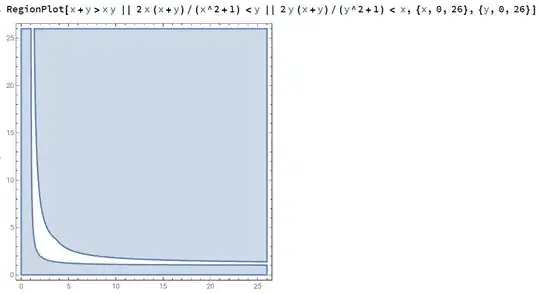
If we pick side3 as $c$ for the inequality $ab < c$ (from Dan's question), this corresponds to, using the expressions for side1/2/3 above, $x+y \gt 2 x y$.
If we pick side2 as $c$ for the inequality $ab < c$ , this corresponds to, using the expressions for side1/2/3 above, $\frac{2x(x+y)}{x^2+1} \lt y$.
If we pick side1 as $c$ for the inequality $ab < c$ , this corresponds to, using the expressions for side1/2/3 above, $\frac{2y(x+y)}{y^2+1} \lt x$.
I tried plotting the union of the inequalities (assuming that the choice of labelling one of the sides, side1/2/3 as "$c$" has a probability of $\frac13$.
This seems to suggest that the probability is close to 1 as we expand the plot to positive quadrant of the real plane (becasue the only requirement is $x \gt 0$ and $y \gt 0$). The unshaded region should be negligible if we take the ratio of shaded to shaded plus unshaded, as we expand the square. Obviously this is wrong, given the number of proofs for the probability to be $\frac12$.
Question: Where am I going wrong in my approach?