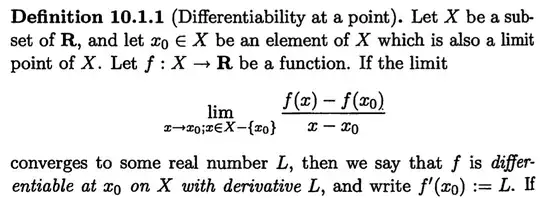Is open set and interiority a necessary condition for differentiability?

Question

I am going by what I am seeing on Wikipedia: In 1D, the standard definition for differentiability is,

A function $f:U\to\mathbb{R}$, defined on an open set $U\subset\mathbb{R}$, is said to be ''differentiable'' at $a\in U$ if the derivative $$f'(a)=\lim_{h\to0}\frac{f(a+h)-f(a)}{h}$$ exists.

Other times, $a$ is defined to be a point which is in the interior of a not necessarily open domain.

However, when I read some other references such as Terence Tao's Analysis I, this assumption does not seem to exist and I don't think it is a mistake or an omission.

Can someone help me understand whether openness and interiority are necessary in order to define differentiability?

Answer 1

You have three definitions of differentiability:

1. For functions $f : U \to \mathbb R$ with an open $U$ and $a \in U$.

2. For functions $f : D \to \mathbb R$ with an arbitrary $D$ and an interior point $a$ of $D$.

3. For functions $f : X \to \mathbb R$ with an arbitrary $X$ and a limit pont $a \in X$ (Tao).

Clearly 3. is the most general definition which covers 2. (since each interior point of $D$ is a limit point of $D$), and 2. covers 1. because each point of an open $U$ is an interior point of $U$.

In contrast to 1. and 2. Tao's definition covers the differentiability of function $f : [a,b] \to \mathbb R$ at the boundary points $a, b$ of closed intervals. This is certainly useful. In many books boundary points are treated as separate cases by introducing the concepts of left hand and right hand derivatives.

However, Tao's definition also covers more exotic cases like functions $f : \mathbb Q \to \mathbb R$ (note that each rational number is a limit point of $\mathbb Q$). Whether one considers this to be useful is everybody's personal opinion.

Note that Tao's definition does not cover isolated points of $X$. For such points there does not exist limit $\lim_{x \to a, x \in X \setminus \{a\}}\frac{f(x)- f(a)}{x-a}$.

Sometimes one can also find the following definition based on 1. :

$f : X \to \mathbb R$ is differentiable in $a \in X$ if there exists an open neighborhood $U$ of $a$ in $\mathbb R$ and function $\phi : U \to \mathbb R$ such that $\phi \mid_{U \cap X} = f \mid_{U \cap X}$ and $\phi$ is differentiable at $a$.

It seems obvious to define $f'(a) = \phi'(a)$, but for an isolated point $a$ this does not make sense because any function $\phi$ defined on a sufficiently small open neighborhood $U$ can be used.

However, for a limit point $a$ of $X$ we obviously get $$\lim_{x \to a, x \in X \setminus \{a\}}\frac{f(x)- f(a)}{x-a} = \phi'(a) .$$

This shows that differentiability (in a limit point) in the above sense implies differentiability in Tao's sense.

Also the converse is true for a limit point $a$. In fact, let $f : X \to \mathbb R$ be differentiable at $a$ in Tao's sense. Define $$\phi: \mathbb R \to \mathbb R, \phi(x) = \begin{cases} f(x) & x \in X \\ f(a) + f'(a)(x-a) & x \notin X\end{cases}$$ You can easily check that $\phi$ is differentiable at $a$ and $\phi \mid_X = f$. Moreover, $\phi'(a) = f'(a)$.

If you want, have a look at Quotient Rule: Why does Tao assume $g$ is non-zero on $X$? You will see that Tao's definition sometimes implicitly occurs when one considers the quotient rule.

Can someone help me understand whether openness and interiority are necessary in order to define differentiability?

It is not necessary for functions defined on some $X \subset \mathbb R$. Tao's definition has benefits as explained above.

However, when we deal with multivariable functions $f: X \to \mathbb R$ defined on some $X \subset \mathbb R^n$, we are well advised to consider only interior points of $X$ as done in the paper linked in your question. We could define differentiability in limit points, but the problem is that in general we do not get a well-defined derivative $f'(a)$. Such a derivative is a linear map which allows to approximate $f$, but is is not representable as a limit as in the case $n = 1$. For interior points it is easy to see that we get a well-defined $f'(a)$. One could also consider points which are no interior points of $X$ at the price of rather technical assumptions on $a$ and $X$, and that is why it is usually not done in textbooks on multivariable calculus.

Answer 2

Short answer:

No. Openness and interiority are not necessary for defining differentiability. Both the definitions can be considered correct, depending on your preference and context, and they do match on "nice enough" functions, even though there might be some edge cases.

Long(er) answer:

As you probably have noticed, the first definition definitely has an issue when you might need to define differentiability on a set that is not open in $\mathbb{R}$. And this might turn out to be sometimes important. (For an example, see the wikipedia section Manifold with boundary here. We have to deal with what differentiability on an open set of $\mathbb{R}$ intersected with a half-plane, means in that context.)

The usual way of extending the first definition I have seen quite frequently, to define a function $f: X\longrightarrow \mathbb{R}$ to be differentiable on a (not necessarily open) set $X$ is, if the domain can be extended to an open set. That is, if there exists a differentiable function $F$ on an open set $U$ containing $X$ such that $F$ is differentiable (by the first definition) and $F\bigg|_X = f$.

This can help extend the notion of differentiability to non-open sets, but it still need not agree with Terrence Tao's definition. As an example, consider the function $f:[0,\infty) \longrightarrow \mathbb{R}$ where $f(x) = e^{-1/x}$. This is differentiable at $0$ according to the second definition, but not according to the (extension of the) first.

So, as I said, which definition is the "correct" one can depend on the context. For most "nice enough" functions that you might come across, these two definitions tend to agree, and they definitely do so when the domain is an open set in $\mathbb{R}$.

Answer 3

This answer is not really a new one: its aim is only to show that the three definitions in Paul Frost's answer are indeed aspects of the same modern definition of limit, thus let's proceed and see why it is so.

Preliminary considerations

Let $U\subseteq \Bbb R$ and $f: U\to \Bbb R$ be a real valued function of a real variable: moreover let $a\in \overline U$ (here $\overline U$ is the closure of $U$) and $\{x_n\}_{n\in\Bbb N}\subset \Bbb R$ be a sequence of real numbers such that $x_n{\to}a$ as $n\to\infty$. Then, from the definition of limit superior and inferior of a sequence (see for example [2], chapter III, §4 pp. 100-107) $$ \exists\lim_{n\to\infty }\frac{f(x_n)-f(a)}{x_n-a}\in\Bbb{\overline R} \iff\liminf_{n\in \Bbb N} \frac{f(x_n)-f(a)}{x_n-a} =\limsup_{n\in \Bbb N} \frac{f(x_n)-f(a)}{x_n-a}. \label{1}\tag{$\ast$} $$ Now, since $$ \begin{align} \liminf_{n\in \Bbb N} \frac{f(x_n)-f(a)}{x_n -a} & \triangleq \sup_{n\ge 0} \inf_{k \ge n} \frac{f(x_k)-f(a)}{x_k-a}\\ \limsup_{n\in \Bbb N} \frac{f(x_n)-f(a)}{x_n-a} & \triangleq \inf_{n\ge 0} \sup_{k \ge n} \frac{f(x_k)-f(a)}{x_k-a}, \end{align}\text{ and} \label{2}\tag{$\ast\ast$} $$ the equality at right side member of \eqref{1} implies that in order to define in full generality the limit of the incremental ratio we must define in full generality the limit superior and the limit inferior in \eqref{2}, i.e. not only for numerable sequences.

A general definition of limit

The proposal at the end of the preceding section is precisely achieved by the theory of nets, also called the Picone, Shatunovskii, Moore and Smith theory of convergence (see for example the Q&A [1] and the references cited therein) from the names of its founders. In order to understand this theory we need the concept of a directed set (here we'll use the notion of downward directed set in order to simplify the notation and emphasise the formal analogies): this is a set $I$ such that

1. if, for every three objects $i^\prime, i^{\prime\prime}, i^{\prime\prime\prime}\in I$, we have $i^\prime\succcurlyeq i^{\prime\prime}$ and $i^{\prime\prime}\succcurlyeq i^{\prime\prime\prime}$ then it is also $i^\prime\succcurlyeq i^{\prime\prime\prime}$, and
2. for every two objects $i^\prime, i^{\prime\prime}\in I$ there exists an object $i^{\prime\prime\prime}$ such that $i^\prime\succcurlyeq i^{\prime\prime\prime}$ and $i^{\prime\prime}\succcurlyeq i^{\prime\prime\prime}$.
3. for every $i\in I$ then $i\succcurlyeq i$.

In order to see ho the theory of nets applies to our case as a generalisation of \eqref{1} and \eqref{2}, let's define a net suitable for our purposes. Consider the set of $\mathscr{I}_a$ of open intervals containing $a$ in their interior and define the family of sets $I_a$ as $$ I_a = \big\{ h_a =(\mathscr{h}_a\cap D)\setminus\{a\} \mid \mathscr{h}_a\in\mathscr{I}_a \big\}. $$ It is simple to prove that $I_a$ is a directed set respect to inverse set inclusion relation$\subseteq$, i.e. $$ \subseteq\; \equiv\; \succcurlyeq\quad\text{if } I\equiv I_a $$ Then, by using this relation and expiating the forma analogy by $\le$ and $\succcurlyeq$, it is possible to generalise the concepts limit superior and inferior of the incremental ratio beyond the boundaries given by sequences: precisely $$ \begin{align} \liminf_{x\in h_a \in I_a} \frac{f(x)-f(a)}{x -a} & \triangleq \sup_{\substack{h_a^\prime\subseteq h_a\\ h_a\in I_a}} \inf_{ \substack{ x\in h_a^{\prime\prime} \\ h_a^{\prime\prime}\subseteq h_a^\prime\\ h_a^{\prime\prime}\in I_a}} \frac{f(x)-f(a)}{x-a}\\ \\ \limsup_{x\in h_a \in I_a} \frac{f(x)-f(a)}{x-a} & \triangleq \inf_{\substack{h_a^\prime\subseteq h_a\\ h_a\in I_a}} \sup_{ \substack{ x\in h_a^{\prime\prime} \\ h_a^{\prime\prime}\subseteq h_a^\prime\\ h_a^{\prime\prime}\in I_a}} \frac{f(x)-f(a)}{x-a}, \end{align} \text{ and} \label{3}\tag{$\ast\ast\ast$} $$ and the definition of limit follows by consequence.

Notes

• This question is not really about the conditions needed for the definition of differentiability of a real valued function: indeed, this is a question of what is needed for a meaningful definition of limit.

• The theory of nets and the theory of filters (see below) have also another important advantage: they show explicitly that the concept of limit is a matter of order relations on the codomain: a topology on the domain is not strictly needed, being only necessary the one of directed set, or even less, since the third axiom above can be dropped without consequences.
  This is also why a definition of limit by using $\limsup$ and $\liminf$ can be said "the most general": these two related quantities always exists for real valued functions, i.e. for functions whose codomain is a totally ordered set, even if they are not equal and thus the limit tout court does not exists. This is also the reason for which in the direct method in the calculus of variation, only $\limsup$ or $\liminf$ of the minimising/maximising sequences are considered.

• The same answer above could have been written by using the language of Cartan's filters, which is the second modern theory of convergence. The two theories are exactly equivalent, except for one fact: while, assuming the axiom of choice, the existence of ultrafilters, i.e. maximal filters that contain each other filter, can be proved, this is not possible for nets.

References

[1] Mathematics StackExchange Q&A: "Definition of limit using ordered variables".

[2] Emanuel Fischer (1983), "Intermediate Real Analysis", Undergraduate Texts in Mathematics, Berlin-Heidelberg-New York: Springer-Verlag, xiv+770, ISBN 0-387-90721-1, DOI: 10.1007/978-1-4613-9481-5, MR681692 (84e:26004), Zbl 0506.26002.