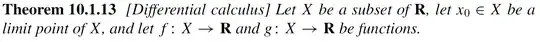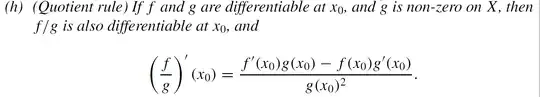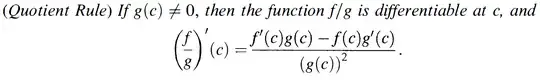Tao (Analysis I, 2022, p. 220):
Why can't Tao just assume $g(x_0)\neq 0$?
Wouldn't the conclusion still hold if we changed the assumption "$g$ is non-zero on $X$" to "$g(x_0)\neq 0$"?
In contrast, Bartle & Sherbert (2011, Introduction to Real Analysis, p. 163f):
Why do Bartle & Sherbert use the assumption $g(c)\neq0$ (as I'd expect) but Tao doesn't?
Every Author & every Book will use some convenient ways to Define the real numbers , then Define limits , Continuity , Derivatives , Etc.
Axioms involved might vary a little here & there.
Such ways are "Essentially Equivalent" , with at most minor variations.
Here , "Tao" uses one way while "Bartle & Sherbert" use some other way , which are "Essentially Equivalent" when we think about it.
Consider that Tao uses the more general "Sub-Sets" of $R$ & "limit Points" , when talking about Continuity & Derivatives & Etc.
Compare that with Bartle & Sherbert , who use the less general "Intervals" & "limits" , when talking about Continuity & Derivatives & Etc.
Even earlier in the theory , Tao uses "Cauchy sequence" to introduce real numbers.
Compare that with Bartle & Sherbert , who use "Completeness Property" to introduce real numbers earlier in the theory.
Naturally , the variations will later dictate how the theorems are stated & proved.
We can see that Tao uses limit Point & Non-Zero $g$ in the Sub-Set , when stating the Quotient rule. The Proof is hinted at in the Exercise 10.1.4 (2016 Edition) where it says "use the limit laws in Proposition 9.3.14"
Page 223 (2016 Edition) :
"Proposition 9.3.14 (Limit laws for functions). Let $X$ be a subset of
$R$, let $E$ be a subset of $X$, [....] If $c$ is a real number, then $cf$ has a limit $cL$ at $x_0$ in $E$. Finally, if $g$ is non-zero on $E$ (i.e., $g(x) \ne 0$ for all $x ∈ E$) and $M$ is non-zero , then $f/g$ has a limit $L/M$ at $x_0$ in $E$."
So here too , we have Non-Zero $g$ in the Sub-Set , not just at a Point.
Proof of that Proposition refers to Theorem 6.1.19 (Limit Laws) in Page 132 (2016 Edition) :
Here too the Condition for $a_n/b_n$ is that $b_n \ne 0$ for all $n$.
In short , the earlier theorems (which Tao wants to use to State & Prove the quotient rule) already use Non-Zero $g$ at all Points in the Sub-Set , which carries over to the later theorems , including the quotient rule.
Compare with Bartle & Sherbert , who state the quotient rule with Interval $I$ & Non-Zero $g(c)$ at Single Point.
The Proof given (Page 164) then uses the new Interval $J$ where $g$ is always Non-Zero , not just at a Single Point.
This $J$ uses theorem 4.2.9 to claim Non-Zero $g$ at all Points.
That theorem (Page 115) says that (A) at a Point $x=c$ , when limit $lim (f) < 0$ , then there is a neighborhood where $f < 0$ always (B) at a Point $x=c$ , when limit $lim (f) > 0$ , then there is a neighborhood where $f > 0$ always
In short , Bartle & Sherbert take Non-Zero $g$ at a Point & then show that we must have Non-Zero $g$ in some Interval (not just at that Point) for quotient rule.
We can then see that Both ways are Equivalent : One way apriori takes Non-Zero $g$ at all Points , the other way takes Non-Zero at a Point & then shows that we must have Non-Zero $g$ at all Points.
Why Tao wants Non-Zero in Sub-Set ? To use the Previous theorems which require it. Tao has no easy theorem to convert "Non-Zero at Point" to "Non-Zero in Sub-Set" , which is required for quotient rule.
Why Bartle & Sherbert uses Non-Zero at Point ? There are Previous theorems which easily convert "Non-Zero at Point" to "Non-Zero in Interval". That Criteria is required for quotient rule.
Why can't Tao just assume $g(x_0)\neq 0$?
Simply because he considers functions having a common domain $X$ and the quotient $f/g$ is only defined if $g(x) \ne 0$ for all $x \in X$. See Definition 9.2.1 (Arithmetic operations on functions).
Wouldn't the conclusion still hold if we changed the assumption "$g$ is non-zero on $X$" to "$g(x_0)\neq 0$"?
In some sense yes, but at the price of being more technical concerning the domain of $f/g$ (which in general will no longer be a function defined on all of $X$).
Why do Bartle & Sherbert use the assumption $g(c)\neq0$ (as I'd expect) but Tao doesn't?
Essentially they do the same as Tao. In Section 5.2 (Combinations of Continuous Functions) they define $f/h$ for functions $f, h : A \to \mathbb R$ such that $h(x) \ne 0$ for all $x \in A$. See Theorems 5.1.1 and 5.2.2.
However, they give a modified interpretation of $f/h$ after Theorem 5.2.2:
Remark. To define quotients, it is sometimes more convenient to proceed as follows. If $\varphi : A \to \mathbb R$, let $A_1 := \{x \in A : \varphi(x) \ne 0 \}$. We can define the quotient $f/\varphi$ on the set $A_1$ by
(1) $\phantom{xxxxxxxx} \dfrac{f}{\varphi}(x) := \dfrac{f(x)}{\varphi(x)}$ for $x \in A_1$.
Observe that is nothing else than the original definition (which agrees with Tao's) applied to the restrictions of $f$ and $\varphi$ to the set $A_1 \subset A$ on which $\varphi$ is non-zero.
When Bartle & Sherbert come to the derivative (Section 6.1), they do something more special than Tao.
Tao defines the differentiability of a function $f : X \to \mathbb R$ at a limit point $x_0$ of an arbitrary set $X \subset \mathbb R$ (Definition 10.1.1), but Bartle & Sherbert only consider functions $f :I \to \mathbb R$ whose domain is an interval. However, they write
Note It is possible to define the derivative of a function having a domain more general than an interval (since the point $c$ need only be an element of the domain and also a cluster point of the domain) but the significance of the concept is most naturally apparent for functions defined on intervals. Consequently we shall limit our attention to such functions.
This would reproduce Tao's definition.
Anyway, there is a formal problem with the quotient rule as stated in Theorem 6.1.3.
If $g(x) = 0$ for some $x \in I$, then the domain $I_1$ of $f/g$ is in general no longer an interval. Thus the quotient rule needs to use the more general definition in the above note. Certainly there exists an interval $J$ such that $c \in J \subset I_1$ (because $g(c) \ne 0$ and $g$ is continuous at $c$) and this gives a reasonable interpretation of $f/g$ being differentiable at $c$, but formally it does not comply with the "official" definitions given in the book.
Conclusion.
There is no essential difference in Tao's and Bartle & Sherbert's variants of the quotient rule.
Tao is very clear about the domain of $f/g$ by requiring that $g$ is non-zero on $X$, but could have used the alternative definition of $f/g$ to get Bartle & Sherbert's result.
Bartle & Sherbert are somewhat vague concerning the domain of $f/g$ and therefore would have to be more precise concerning the interpretation of $f/g$ being differentiable at $c$. Actually, they have to consider the restrictions of $f$ and $g$ to the subset $I_1 \subset I$ which in general is no interval.
"Why doesn't he just assume $g(x_0) \neq 0$?"
Answer: For the question to make sense! If there is some point in the domain where $g$ is zero, then what does $\frac{f}{g}$ even mean at that point? How do you define $\frac{f}{g}$ at a point where $g$ is zero?
He could actually omit this restriction, since it is implicit when we even mention $\frac{f}{g}$
