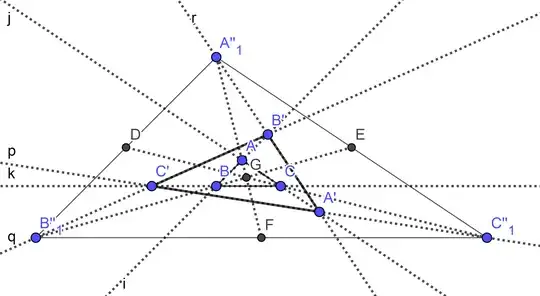
Given a triangle $ABC$, consider the triangle $DEF$ where $B$ is the midpoint of $AD$, $A$ is the midpoint of $CF$ and $C$ is the midpoint of $BE$. Show that the barycenters of $ABC$ and $DEF$ coincide.
Obs: Use plan geometry
I have by vectors. I need by plan geometry
The midpoint is given by $\vec{X}=\dfrac{\vec{X}+\vec{Y}}{2}$
$\vec{A}=\dfrac{\vec{C}+\vec{F}}{2}$
$ \vec{B}=\dfrac{\vec{A}+\vec{D}}{2}$
$\vec{C}=\dfrac{\vec{B}+\vec{E}}{2}$
$ \therefore \dfrac{\vec{A}+\vec{B}+\vec{C}}{3}= \dfrac{\vec{D}+\vec{E}+\vec{F}}{3} \implies$
$\vec{G}_{ABC}=\vec{G}_{DEF}$