In $\Delta ABC$ Can any one give me a hint to Prove that the centroid $G$ divides $A$ and Mid point of $BC$ in the ratio $2$:$1$ Using only Plane Geometry.
-
1What is the geometric definition of centroid? – André Nicolas Jun 11 '15 at 02:55
-
possible duplicate of Medians of a triangle and similar triangle properties – user26486 Jun 11 '15 at 04:39
4 Answers
Alternative proof, a bit more interesting (see picture):
$\frac{CB}{CF}=\frac{CB_1}{CA}$, so $BB_1 || FA$, so $\frac{A_1B}{A_1F}=\frac{A_1G}{A_1A}=\frac{1}{3}$.
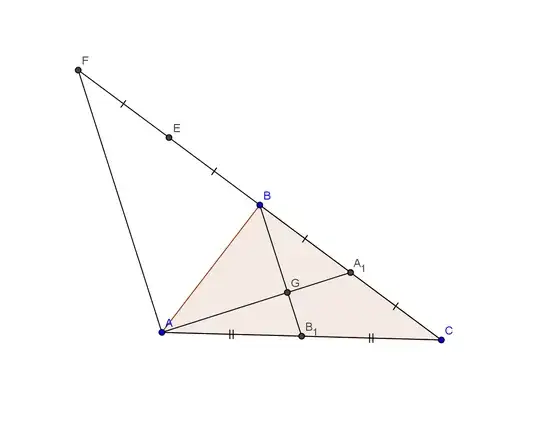
- 11,519
Let $A_1,B_1$ be midpoints of $BC, AC$, respectively. Then $AA_1\cap BB_1= G$.
$\triangle CB_1A_1\sim \triangle CBA$, because $\angle C$ is common and $\frac{CB_1}{CA}=\frac{CA_1}{CB}=\frac{1}{2}$,
so $\frac{A_1B_1}{AB}=\frac{1}{2}$ and $A_1B_1||AB$ and $\angle BAA_1=\angle AA_1B_1$ and $\angle ABB_1=\angle A_1B_1B$,
so $\triangle ABG\sim\triangle A_1B_1G$ with ratio $\frac{A_1B_1}{AB}=\frac{1}{2}$, so $\frac{BG}{GB_1}=\frac{AG}{GA_1}=\frac{1}{2}$.
- 11,519
Let $L$, $M$ and $N$ be the midpoints of $AB$, $BC$ and $AC$ and $G$ be the centroid.
- The median divides the area of a triangle into 2 parts of equal area.
- $S_{\triangle ABM} = S_{\triangle ACM} $ since $AM$ is median of $S_{\triangle ABC}$.
- $S_{\triangle GBM} = S_{\triangle GCM} $ since $GM$ is median of $S_{\triangle GBC}$.
- Thus by subtraction, $S_{\triangle ABG} = S_{\triangle ACG} $.
- By symmetry we have $S_{\triangle ABG} = S_{\triangle ACG} = S_{\triangle BCG} $.
- So the area of $\triangle BCG$ is one third of the area of the whole triangle $\triangle ABC$. $S_{\triangle ABC} = 3\cdot S_{\triangle BCG}$
- So $AM = 3 \cdot GM$. And we can conclude now.
- 38,565
- 3,847
Let $AA_1$ and $BB_1$ be two medians, and $G$ their intersection. Denote by $A_2$ respectively $B_2$ the midpoints of $AG$ respectively $BG$.
Then, since $A_1B_1$ is midline in $CBA$ and $A_2B_2$ is midline in $GBA$ we have that both are parallel to $AB$ and half of $AB$. This shows that the oposite sides $A_1B_1$ an $A_2B_2$ in the quadrilateral $A_1B_1A_2B_2$ are parallel and equal. This shows that $A_1B_1A_2B_2$ is parallelogram.
The claim follows from the fact that the diagonals of this parallelogram half eachother.
- 134,609