2

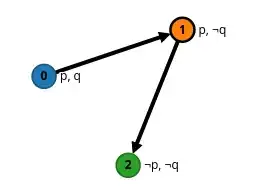
I have constructed the following Kripke model for this problem:

enter image description here

My idea is the following: Implication is false iff we have $ \top \implies \bot$.

For world $0$, we have that $p$ is true. Now we need to evaluate $\Box \Diamond q$. For world $0$, $\Box \Diamond q$ is true iff $\Diamond q$ is true in every world which is reachable from world $0$ (that would be world $1$). Now, in world $1$, $\Diamond q$ is true if $q$ is true in at least one world reachable from world $1$, and the only such world is $2$. Now, since $q$ is false in world $2$, we can say that $\Diamond q$ is false in $1$, and so $\Box \Diamond q$ is false in $0$. We have our implication $\top \implies \bot$.

My questions are:

  1. Obviously, the value of $q$ in world $1$ is $\neg q$. However, we don't really need that value for anything because we only use world $1$ as an "intermediary" world of sorts, right?

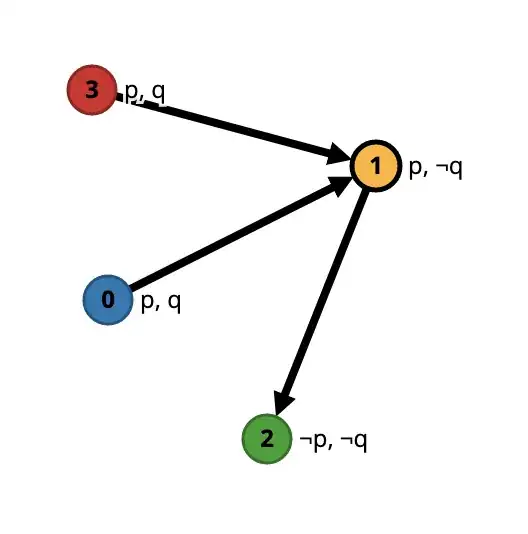
  2. Can different worlds in the same Kripke model have the same truth values for the same variables? I.e., could I have added a world $3$ with $p,q$ as values for $p,q$?

Chris Grossack
  • 42,257
l0ner9
  • 623

1 Answers1

1

  1. You're exactly right. For the purposes of evaluating the truth of $\square \lozenge q$ in world $0$, it doesn't matter what world $1$ thinks about $p$ or $q$ (although it would matter if there were an edge from $1$ to itself. Do you see why?)

  2. It's completely fine for different worlds to have the same truth values. For instance, you can have something like this:

a kripke model

where not only do $0$ and $3$ agree on all the primitive propositions ($p$ and $q$) they actually agreee on all modal formulas! (This is a nice exercise)

I hope this helps ^_^

Chris Grossack
  • 42,257
  • 1
    Thank you very much for your answer! Another question arose though:

    $\Box p$ is true in the current world if it is true in all worlds reachable from the current world. However, if no world is reachable from the current world, we say that $\Box p$ is vacuously true in the current world.

    What about $\Diamond p$? It's true in the current world if it's true in at least one world reachable from the current world. However, what if no such world exists (that is reachable from the current world)? Is it vacuously false?

     – l0ner9 Jun 21 '23 at 09:04
  • 1
    @l0ner9 -- that's also correct. If $w$ doesn't see any worlds, then vacuously $w$ thinks $\square p$ is true, and that $\lozenge p$ is false. Another way to see this is to use the relation $\lozenge p = \lnot \square \lnot p$. – Chris Grossack Jun 21 '23 at 09:10