The area between parabolic lines inside a square

Question

The following square has edges of size $1$ and I'm trying to find the area of the blue region trapped between the parabolic curves created by the straight lines (number of lines is technically infinite).

I assume that the simplest way to go about this is to use integration based on the parabolic equations that the lines create, but is there any more fundamental way of solving this maybe using infinite series and limits? Or at least explaining the integral solution using differentiation and limits.

P.S. You can imagine that a line is drawn at the point $\dfrac 1n$ of one edge to the point $1-\dfrac1n$ of the other edge where $n$ varies from $1$ to infinity.

Answer 1

Consider a square $ABCD$ and four points $PQRS$ on its sides such that $AP=BQ=CR=DS$ (see figure below). $PQRS$ is a square with the same center $O$ as $ABCD$, hence $O$ lies on the circumcircle of triangles $APQ$, $BQR$, $CRS$, $DSP$.

But the focus of a parabola lies on the circumcircle of the triangle formed by any three of its tangents, hence $PQ$ is tangent to the parabola with focus $O$ and also tangent to $DA$ and $AB$, $QR$ is tangent to the parabola with focus $O$ and also tangent to $AB$ and $BC$, and so on.

Let's consider the parabola with focus $O$, tangent to $DA$ and $AB$. By symmetry, its axis is line $AC$ and its directrix passes through $A$, because two perpendicular tangents to a parabola meet on the directrix. Its vertex $V$ is the midpoint of $OA$ (because $O$ is also the midpoint of the chord of contact $BD$).

If this parabola meets one of the other parabolas at $E$ (see figure below), we can find $OE$ from: $$ OE=EH={EG\over\sqrt2}={1-OE\over\sqrt2} \implies OE=\sqrt2-1. $$ It is then not difficult to find the length of $$ OL=LE={OE\over\sqrt2}=1-{1\over2}\sqrt2 \quad\text{and}\quad LV=OV-OL={3\over4}\sqrt2-1. $$ The area of interest is then the sum of square $EIJK$ and of four parabolic segments whose area can be computed via Archimedes' theorem (area of parabolic segment $IEV$ is ${4\over3}\cdot$ area of triangle $IEV$): $$ area=4OL^2+4\cdot{4\over3}LE\cdot LV={8\sqrt2-10\over3}. $$

Answer 2

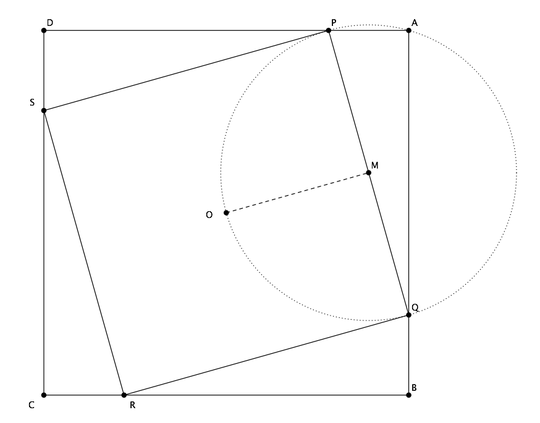
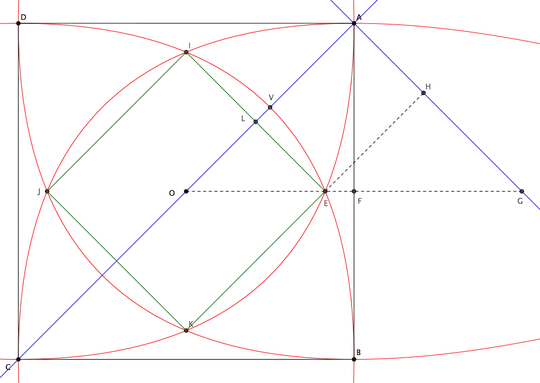
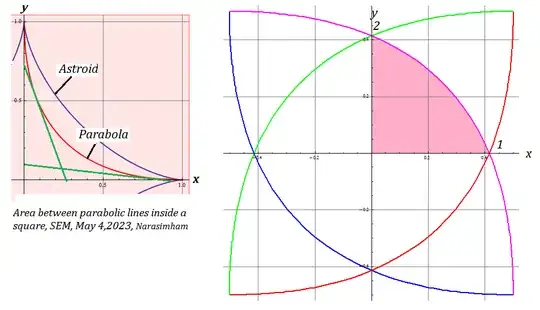
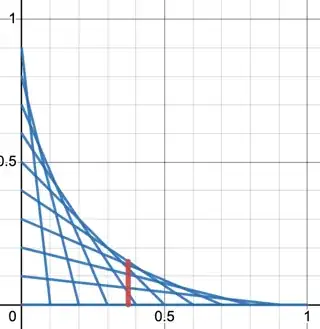
So, I (very randomly) happen to have been playing with this exact problem a few days ago. Here is my approach. Focusing first on the set of lines from the $y$-axis down to the $x$-axis, we have the following.

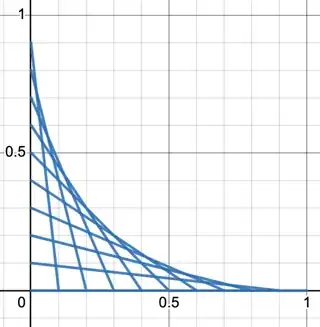
Each line that goes from $(t,0)$ to $(0,1-t)$ has the equation

$$ y = \frac{t-1}{t} x + 1-t = x - \frac{1}{t}x +1 - t$$

for $t\in [0,1]$. Then we want to know what line (i.e. which $t$), for a given $x$ has a maximum $y$ value. Thus, we need to optimize with respect to $t$.

$$\frac{dy}{dt} = \frac{1}{t^2}x-1$$

Setting this equal to zero, to find critical points, we get $t = \sqrt{x}$, and this is a maximum! Thus,

$$ y = x - \frac{1}{\sqrt{x}}x +1 - \sqrt{x} = x-2\sqrt{x} +1$$

is the curve that is the maximized line at each $x$ value. (As is stated in other answers, this is equivalent to $\sqrt{x}+\sqrt{y}=1$)

Now that we have the curve, we just need to integrate properly. Noticing that the curves in your original image intersect at $x, y = \frac{1}{2}$. And symmetry tells us that the $x$ value where $y$ is $\frac{1}{2}$ is the same as the $y$ value where $x$ is $\frac{1}{2}$, which is $\left(1-\sqrt{\frac{1}{2}} \right)^2$.

So to find the area of the shaded region inside all four of the transformed versions of this curve, we can find the area of the purple region in the image below and multiply by four.

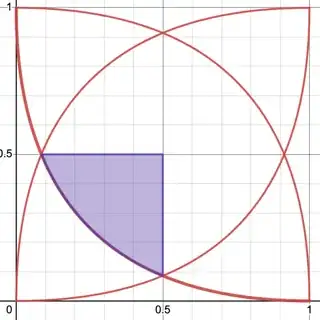
This will be done by solving (with wolfram alpha, since this is not the interesting part) $$\int_{\left(1-\sqrt{\frac{1}{2}} \right)^2}^\frac{1}{2} \frac{1}{2} - \left( x-2\sqrt{x} +1\right) dx = \frac{1}{6} (4 \sqrt{2}-5)$$

And so the total area is $\frac{2}{3} (4 \sqrt{2}-5)\approx 0.4379$. This is also what Intelligenti pauca got, when they used only geometry, beautifully.

Answer 3

Background:

The astroid is an envelope enclosed between a vertical wall and floor made by a sliding ladder of constant length L. $a=1.$ $$ (x/a,y/a) = (\cos^3 t, \sin ^3 t); x^ \frac 23 + y^ \frac 23 = a^ \frac 23; \tag 1 $$

HINT:

For Parabolic arc

A parabolic arc envelope occurs by variable ladder length when maximum length L is at $(0,90) $ deg and minimum length $ L/\sqrt {2}$ occurs at $45^\circ $ to floor.

We may say that the parabolic arc has a property of constant $ (x , y) $ intercepts sum at least between tangency points at $x,y$ axes. ( Because the parabola expands after tangential contact ). The straight line length varies.

Shifting of axes as given enables finding area in first quadrant. Other three quadrants have same area by symmetry of axes. The magenta parabolic arc has parametrization

$$ (x(t)/a,y(t)/a) = (\frac12- \cos^4 t,\frac12- \sin ^4 t); \tag 2$$

The domain for t is $( t= 0,\pi/2)$

The independent parameters $(t_1,t_2) $ are given from the above parametrization to be

$$ \left(\cos^{-1}\frac{1}{2^ {\frac14}}, \sin^{-1}\frac{1}{2^ {\frac14}}\right) \approx (0.571859,0.998937) \tag 3 $$

and four times the shaded area is

$$ 4 \int_{t1} ^{t2} y(t) x'(t) dt $$

Plug in from (2) and trig substitutions.

EDIT 1:

Derivation of parabolic arc.

${u}$ is shortening in y- axis segment= offset on x-axis. $$ \frac{x}{u}+ \frac{y}{a-u} = 1 \tag {1a}$$ $$ \frac{x}{u/a}+ \frac{y}{1-u/a} = a \tag {1b}$$ Partial differentiate (1 a) w.r.t. $u$ $$ \frac{-x}{u^2}+\frac{y}{(a-u)^2}=0 \tag 2 $$ $$ \frac{u}{a}= \frac{\sqrt x }{\sqrt x + \sqrt y }~; 1- \frac{u}{a}= \frac{ \sqrt y }{\sqrt x + \sqrt y }~; \tag 3 $$ Plug into (1b) and simplify $$ x+y + 2 \sqrt {xy} =a \tag 4 $$

Take square root

$$\sqrt{x}+\sqrt{y}=\sqrt{a} \tag 5 $$