According to the generic theory of linear diffusion processes, i.e time homogeneous Markov processes with independent increments
Itô, Kiyosi; McKean, Henry P. jun., Diffusion processes and their sample paths., Classics in Mathematics. Berlin: Springer-Verlag. xviii, 326 p. (1996). ZBL0837.60001.; section 4.6, Solving ${\mathfrak G} u = \alpha u$, page 128
the Laplace transform $u_\alpha^{(b)}(x) := E\left[ e^{-\alpha \tau_b} | X_0 = x \right]$ of the first hitting time $\tau_b := \inf\{t >0 | X_t > b\} $ of a barrier $b > x >0 $ is given as a unique solution to the following Sturm-Liouville value problem:
\begin{eqnarray} {\mathfrak G} u_\alpha^{(b)}(x) &=& \alpha \cdot u_\alpha^{(b)}(x) \tag{1} \\ \left.u_\alpha^{(b)}(x) \right|_{x=b} =1, && \lim\limits_{x \rightarrow -\infty} u_\alpha^{(b)}(x) = 0 \tag{2} \end{eqnarray}
where ${\mathfrak G}$ is the infinitesimal generator of the process, i.e. ${\mathfrak G} u := \lim\limits_{\epsilon \rightarrow 0} \frac{E_{\cdot} \left[ u(X_\epsilon) | X_0 = x \right] - u }{\epsilon}$ for some smooth function $u : \Omega \rightarrow {\mathbb R} $ with $\Omega$ being the space of events.
We can also find the statement of this theorem in
Alili, L.; Patie, P.; Pedersen, J. L., Representations of the first hitting time density of an Ornstein-Uhlenbeck process, Stoch. Models 21, No. 4, 967-980 (2005). ZBL1083.60064.; Proposition 2.1 page 2-3.
Now, what I did is the following. I decided to apply the result above to some diffusion processes and verify it by a Monte Carlo simulation.In doing so I come to conflicting results and I would like to understand what it is that I did wrong. Here we go:
The geometric Brownian motion:
Here $dX_t = \mu_0 X_t dt + X_t dB_t$ where $B_t$ is the Brownian motion and $\mu_0 \le 1/2$. For this process the infinitesimal generator reads ${\mathfrak G} = \mu_0 x d/dx + 1/2 x^2 d^2/d x^2 $. As such equation $(1)$ takes the following form:
\begin{equation} \left[ \mu_0 x \frac{d}{d x} + \frac{1}{2} x^2 \frac{d^2}{d x^2} \right] u_\alpha^{(b)}(x) = \alpha \cdot u_\alpha^{(b)}(x) \tag{3} \end{equation}
This is an Euler equation so the trial $x^\zeta$ leads to a solution where $\mu_0 \zeta + 1/2 \zeta (\zeta-1) = \alpha $ which is solved by $\zeta = (1/2 - \mu_0) \pm 1/2 \sqrt{(1-2 \mu_0)^2 + 8 \alpha} $. The first boundary condition in $(2)$ leads to the following solution:
\begin{equation} u_\alpha^{(b)}(x) = \left( \frac{x}{b} \right)^\zeta = \left( \frac{x}{b} \right)^{\frac{1}{2} - \mu_0 \pm \frac{1}{2} \sqrt{(1-2 \mu_0)^2 + 8 \alpha}} \tag{4} \end{equation}
From the normalization, i.e. $u_0^{(b)}(x) = 1$ it follows that we need to take the $-$-solution. In this case we also easily verify that the second boundary condition in $(2)$ is satisfied whenever $\alpha > 0 $ as it should be. Therefore the final solution reads:
\begin{equation} u_\alpha^{(b)}(x) =\left( \frac{x}{b} \right)^{\frac{1}{2} - \mu_0 } \cdot \exp\left(-\frac{1}{2} \log(\frac{x}{b}) \sqrt{(1-2 \mu_0)^2 + 8 \alpha}) \right) \tag{5} \end{equation} for $x \le b$.
This is all very good but now I am saying that the function in $(5)$ is not a valid Laplace transform when $x \le b$! By inverting we have:
\begin{eqnarray} \rho_{\tau_b}(t) &:=& {\mathcal L}^{-1}_\alpha \left[ u_\alpha^{(b)}(x)\right](t) \\ &=& \left( \frac{x}{b} \right)^{\frac{1}{2} - \mu_0 } \cdot \frac{1}{8} e^{-\frac{1}{2} (\mu_0 - \frac{1}{2})^2 t} \underline{ {\mathcal L}^{-1}_\alpha \left[ e^{-\frac{1}{2} \log(\frac{x}{b} ) \sqrt{\alpha}} \right](\frac{t}{8})} \tag{6} \end{eqnarray}
We can clearly see that the underlined quantity above does not exist when $ x < b $. Indeed we have ${\mathcal L}^{-1}_\alpha \left[ e^{-A \sqrt{\alpha}} \right](t) = A/(2 \sqrt{\pi} t^{3/2}) \exp(-A^2/(4 t)) 1_{A>0}$. The inverse Laplace transform in question exists only if the boundary value is smaller than the first price contrary to the assumption that we have, i.e. $ x < b $! However, if we forget about this problem and simply replace $\log(\frac{x}{b} ) \rightarrow \log(\frac{b}{x} ) $ in equation $(6)$ then we obtain:
\begin{equation} \rho_{\tau_b}(t) := \frac{\log(\frac{b}{x})}{\sqrt{2 \pi t^3}} \cdot \exp\left( -\frac{1}{2 t} \left[ \log(\frac{b}{x}) - (\mu_0-\frac{1}{2} ) t\right]^2\right) \tag{7} \end{equation}
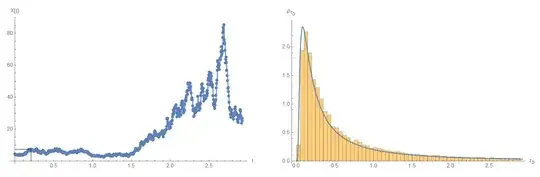
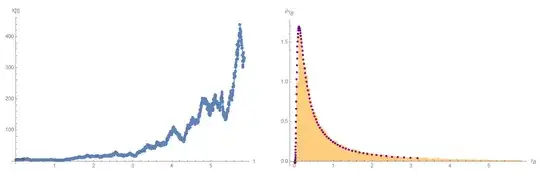
Clearly $(7)$ is the correct result as the Monte Carlo simulation below demonstrates:
(*Monte Carlo simulation of 1st hitting time distribution.*)
mu0 = 1; Clear[Bs]; x = Exp[3/2]; b =
Exp[2]; NN = 750; numInst = 50000;
dt = 1/256 ;
myHist = {};
Do[
Bs = RandomVariate[NormalDistribution[0, 1], NN];
Xs = Drop[FoldList[#1 + mu0 #1 dt + #1 #2 Sqrt[dt] &, x, Bs], -1];
ts = dt Range[1, NN];
tHit = Min[Flatten[Position[Sign[Xs - b], _?(# == 1 &), 1]]] dt;
myHist = Join[myHist, {tHit}];
If[Mod[which, 5000] == 0, PrintTemporary[which]];
, {which, 1, numInst}];
b = Exp[2];
line1 = Line[{{tHit, 0}, {tHit, b}}];
line2 = Line[{{0, b}, {tHit, b}}];
pl1 = ListPlot[Transpose[{ts, Xs}], Joined :> True,
PlotMarkers -> Automatic, Epilog -> {line1, line2},
AxesLabel :> {"t", "X[t]"}];
b =.; pl20 =
Histogram[myHist, {0, NN dt, 0.05}, "PDF",
AxesLabel -> {Subscript[[Tau], b],
Subscript[[Rho], Subscript[[Tau], b]]}];
b = Exp[2];
mpdf[t_, x_, b_, mu0_] :=
1/Sqrt[2 Pi] Log[b/x] 1/
t^(3/2) Exp[-1/(2 t) (Log[b/x] - (mu0 - 1/2) t)^2];
pl21 = Plot[mpdf[t, x, b, mu0], {t, 0, NN dt}, PlotRange :> All];
b =.; pl2 = Show[pl20, pl21];
GraphicsGrid[{{pl1, pl2}}]
Where is the error in my understanding of the results of the theory of linear diffusion processes?