Find the rotation symmetries of cube in terms of the four long diagonals.

Question

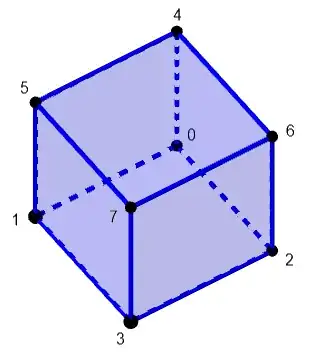
Request to vet the thorough description of the cube's rotations, and help in the second way to represent the rotation symmetries of the cube.

Have the usual way of describing the $24$ non-trivial rotation symmetries of a cube in terms of the eight vertices.
Also, represent the cube in terms of configurations of vertices by describing the two $x-z$ planes in the counter-clockwise direction, starting with farthest point in the $x,$ and $z$ directions.
For the purpose of stating configurations, use two square brackets, each containing $4$ vertices.
Say, the initial configuration as given below is: $[EHCD][FGBA].$
Say, for the below cube, have three non-trivial rotations along each of the $3$ axis, formed by the midpoints of opposite faces, as:

(A). Along the midpoints of faces along the $x-z$ axis, in counter-clockwise direction, i.e. the faces: $EHCD, FGBA$:

1. $(EHCD)(FGBA),$ final configuration : $[DEHC][AFGB],$
2. $(EC)(HD)(FB)(GA),$ final configuration : $[CDEH][BAFG],$
3. $(EDCH)(FABG),$ final configuration : $[HCDA][GBAF].$

(B). Along the midpoints of faces along the $x-y$ axis, in counter-clockwise direction, i.e. the faces: $CBGH, DAFE$:

1. $(CBGH)(DAFE),$ final configuration : $[FGHE][ABCD],$
2. $(CG)(BH)(DF)(AE),$ final configuration : $[ABGF][DCHE],$
3. $(CHGB)(DEFA),$ final configuration : $[DCBA][EHGF].$

(C). Along the midpoints of faces along the $y-z$ axis, in counter-clockwise direction, i.e. the faces: $CDAB, HEFG$:

1. $(CDAB)(HEFG),$ final configuration : $[HGBC][EFAD],$
2. $(CA)(DB)(HF)(EG),$ final configuration : $[GFAB][HEDC],$
3. $(CBAD)(HGEF),$ final configuration : $[FEDA][GHCB].$

Similarly, there are $8$ non-trivial rotations about the diagonally opposite vertices, in $\pm120^o$ counter-clockwise direction.
There are $4$ such vertex pairs.
In the below labelled cube, have: $E-B, C-F, H-A, D-G.$
The symmetries are given by:

(D). About the vertices $C-F$:

1. $(HDB)(EAG),$ final configuration : $[GBCH][FADE],$
   
2. $(HBD)(EGA),$ final configuration : $[ADCB][FEHG],$

(E). About the vertices $E-B$:

1. $(HDF)(CAG),$ final configuration : $[EFGH][DABC],$
   
2. $(HFD)(CGA),$ final configuration : $[EDAF][HCBG],$

(F). About the vertices $H-A$:

1. $(CEG)(FBD),$ final configuration : $[CHGB][DEFA],$
   
2. $(CGE)(FDB),$ final configuration : $[GHEF][BCDA],$

(G). About the vertices $D-G$:

1. $(EAC)(HFB),$ final configuration : $[CBAD][HGFE],$
   
2. $(ECA)(HBF),$ final configuration : $[AFED][BGHC],$

Next, there are six non-trivial edge rotations of $180°,$ about the midpoints of diagonally (long) opposite edges.

(H). Axis about the midpoints of the opposite edges: $H-G, D-A$:
$(HG)(DA)(EB)(CF),$ final configuration : $[BGFA][CHED],$

(I). Axis about the midpoints of the opposite edges: $H-C, F-A$:
$(HC)(FA)(EB)(DG),$ final configuration : $[BCHG][ADEF],$

(J). Axis about the midpoints of the opposite edges: $H-E, B-A$:
$(HE)(BA)(DG)(CF),$ final configuration : $[HEFG][CDAB],$

(K). Axis about the midpoints of the opposite edges: $C-D, G-F$:
$(CD)(GF)(EB)(AH),$ final configuration : $[BADC][GFEH],$

(L). Axis about the midpoints of the opposite edges: $C-B, E-F$:
$(CB)(EF)(HA)(DG),$ final configuration : $[FABG][EDCH],$

(M). Axis about the midpoints of the opposite edges: $E-D, B-G$:
$(ED)(BG)(HA)(CF),$ final configuration : $[DAFE][CBGH],$

Next, is the job to represent the $24$ rotation symmetries using the four diagonals.

Let us call the two representations: $Cub_8,$ and $Cub_4$ respectively.
$Cub_8$ is based on the $8$ vertices, and hence a subset of $S_8.$ While $Cub_4$ is based on the $4$ long diagonals, and hence a subset of $S_4.$ In fact, $Cub_4$ is isomorphic to $S_4.$

Let these four diagonals :$EB, HA, CF, DG,$ be named after the first letters :$E, H, C, D,$ respectively. I.e. the long diagonals are named by the vertices in the initial configuration shown below, in the top $x-z$ plane.

The case of $180^o$ rotations about the midpoints of diagonally opposite edges, seems toughest in the second representation.

There are six such rotations, and each should have a unique representation by a single transposition; but cannot prove it.
So, if a proof could also be provided that each of such $6$ symmetries needs just a single transposition of the four diagonals, then better.
Though, also have $4C2=6$ combinations of the four diagonals, taken two for the purpose of a single transposition.

(H). Axis about the midpoints of the opposite edges: $H-G,D-A> (HD),$ i.e. the transposition of the two long diagonals $HA, DG$ occurs.

(L). Axis about the midpoints of the opposite edges: $C-B, E-F> (EC),$ i.e. the transposition of the two long diagonals $EB, CA$ occurs.

Am sure about the above two symmetries, labelled: (H), (L). But, not about the rest $4$ edge symmetries of $180^o$ rotations, as stated below:

(I). Axis about the midpoints of the opposite edges: $H-C, F-A: ,$

(J). Axis about the midpoints of the opposite edges: $H-E, B-A: ,$

(K). Axis about the midpoints of the opposite edges: $C-D, G-F: ,$

(M). Axis about the midpoints of the opposite edges: $E-D, B-G: ,$

Would be very much helped if some gif as here, be provided.

Answer 1

Notation

Label the vertices of the cube as follows:

\begin{array}{cc} \text{vertex name} & \text{coordinates} \\ \hline 0 & (0,0,0) \\ 1 & (0,0,1) \\ 2 & (0,1,0) \\ 3 & (0,1,1) \\ 4 & (1,0,0) \\ 5 & (1,0,1) \\ 6 & (1,1,0) \\ 7 & (1,1,1) \end{array}

That is, we treat the coordinates as digits of a binary number, also called bits. Vertices at two ends of an edge have names differing by one bit (such as the pair $2=010_2$ and $3=011_2$ or the pair $1=001_2$ and $5=101_2$). Vertices at two ends of a face diagonal have names with just one matching bit (such as the pair $4=100_2$ and $7=111_2$). Vertices at two ends of a body diagonal have names with all bits different, so if one vertex has name $x$ then the other has name $7 - x.$

We can identify each body diagonal by the lower-numbered vertex at an end of the diagonal, so the diagonals are named $0,1,2,3.$

We can describe the "home" orientation of the cube by listing the vertices of the cube by name in increasing numerical order. We can describe any other orientation by replacing each vertex name with the name of the vertex that now lies at the same point. Similar to the notation in the question, we can use square brackets to write the vertices in groups of four and omit commas between vertex names. So the home orientation is $[0123][4567]$ and the result of rotating the face $0123$ so that vertex $0$ moves to the home position of vertex $1$ is $[3012][7456].$

But I will just write the permutations of vertices (eight digits in groups of one or more), since the listing of the orientation can be obtained by permuting the vertices of the home position.

I will also write the permutations of the diagonals as permutations of the digits $0,1,2,3$ which name the diagonals.

Rotations of faces

Take a pair of faces. One face has all $0$s at a particular bit position. The other has all $1$s at that bit position.

Take the vertices around one face in cyclic order. The non-constant bits on that face cycle through two-bit Gray code. The permutation of one $90$-degree rotation is simply the cyclic list of four vertices of one face in a cycle, and the other four vertices in a second cycle. Order the second cycle so that if diagonal $m$ transitions to diagonal $n$ on one face then diagonal $m$ rotates to diagonal $n$ on the other face.

The permutation of the body diagonals is just one of the four-cycles with each vertex name translated to its body-diagonal name; that is, if the vertex name is $n$ and $n>3,$ replace $n$ by $7 - n.$

The remaining permutations are just the square and inverse of the first permutation. For the square we have four two-cycles of vertices; these reduce to two two-cycles of body diagonals when we replace vertex names with their body-diagonal names and eliminate duplicate cycles.

Do this for three pairs of faces.

In the table below, after translating a four-cycle of vertices into the vertices at the opposite ends of the body diagonals, I rewrite the second cycle starting at its lowest-numbered vertex. In later parts of this answer I also rewrite other cycles to start at their lowest-numbered vertex.

\begin{array}{cc} \text{faces} & \text{vertex permutations} & \text{diagonal permutations} \\ \hline 0123,4567 & (0132)(4576) & (0132) \\ & (03)(12)(47)(56) & (03)(12) \\ & (0231)(4675) & (0231) \\ 0145,2367 & (0154)(2376) & (0123) \\ & (05)(14)(27)(36) & (02)(13) \\ & (0451)(2673) & (0321) \\ 0246,1357 & (0264)(1375) & (0213) \\ & (06)(24)(17)(35) & (01)(23) \\ & (0462)(1573) & (0312) \end{array}

Rotations holding vertices fixed

Choose two body-diagonally opposite vertices ($n$ and $7 - n$) to be held fixed.

List the adjacent vertices of one of the fixed vertices. The permutation of vertices is this list in one three-cycle, the other ends of the body diagonals at these three vertices in a matching cycle (diagonal $m$ transitions to the same diagonal $n$ in both cycles) and two singletons for the remaining vertices.

The permutation of body diagonals is the first three-cycle with vertex names replaced by their body-diagonal names.

The other non-trivial rotation around these vertices is the inverse of the first rotation.

Do this for four pairs of vertices.

\begin{array}{cc} \text{vertices} & \text{vertex permutations} & \text{diagonal permutations} \\ \hline 0,7 & (0)(124)(365)(7) & (0)(123) \\ & (0)(142)(356)(7) & (0)(132) \\ 1,6 & (035)(1)(274)(6) & (032)(1) \\ & (053)(1)(247)(6) & (023)(1) \\ 2,5 & (036)(174)(2)(5) & (031)(2) \\ & (063)(147)(2)(5) & (013)(2) \\ 3,4 & (056)(172)(3)(4) & (021)(3) \\ & (065)(127)(3)(4) & (012)(3) \end{array}

Rotations of edges

Choose an edge and the diagonally opposite edge. The diagonally opposite edge is found by taking the names of the first edge and flipping the two bits that are constant on that edge.

For the permutation of vertices, the (single) rotation of these edges has four two-cycles. Each of the two named edges is a two-cycle, and each of the diagonals that does not have a vertex on these edges is a two-cycle.

For the permutation of body diagonals, take one of the edges and convert its vertex names to body-diagonal names. Those two body diagonals are a two-cycle and the other body diagonals are singletons.

\begin{array}{cc} \text{edges} & \text{vertex permutations} & \text{diagonal permutations} \\ \hline 01,67 & (01)(25)(34)(67) & (01)(2)(3) \\ 23,45 & (07)(16)(23)(45) & (0)(1)(23) \\ 02,57 & (02)(16)(34)(57) & (02)(1)(3) \\ 13,46 & (07)(13)(25)(46) & (0)(13)(2) \\ 04,37 & (04)(16)(25)(37) & (03)(1)(2) \\ 15,26 & (07)(15)(26)(34) & (0)(12)(3) \end{array}

It's all quite mechanical and the permutations can be worked out without diagrams. The main trick is simply to be able to quickly know which vertices are adjacent to which and which are at opposite ends of a body diagonal. Any labeling would suffice if you can memorize all these relationships, but the labeling in this answer makes the relationships evident through arithmetic.