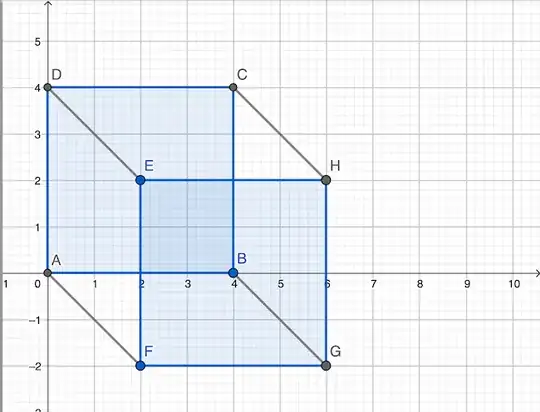
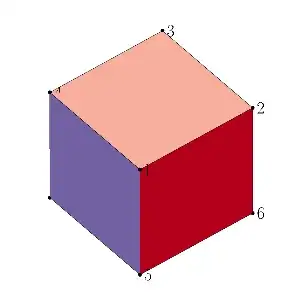
Given a cube am facing great difficulty in visualising rotation symmetries along the axis formed by the midpoints of diagonally opposite edges.
Given two diagonally opposite edges, need consider the rest of coplanar edges, and the two long diagonals formed through them.
Need to swap the vertices of these long diagonals, for order $2$ rotation symmetry, apart from swap of the two vertices of each diagonally opposite edge.
And need to find the rotational symmetry being given by the axis formed by the midpoints of edges determined by the vertices $A,F$ and $C,H$ respectively. Then, the correct answer is given by the rotational symmetry: $(AF)(CH)(DG)(BE).$
Say, here have great difficulty in visualising how the vertices $D,G$ get swapped.
Have found a link on desmos at: cube
If could modify parameters here, to visualise the rotation symmetry given above, then would be able to visualise easily. Or, if could provide some even better visualization tool.