Consider the following two Dirichlet series
$$C_3(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N 1_{n=p^k}\, \log(n)\, n^{-s}\right),\quad\Re(s)>1\tag{1}$$
$$K_\Omega(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N 1_{n=p^k}\, \Omega(n)\, n^{-s}\right),\quad\Re(s)>1\tag{2}$$
where $1_{n=p^k}$ is the prime-power indicator function which returns the value $1$ if $n$ is a prime-power and zero otherwise and $\Omega(n)$ counts the number of non-distinct primes in $n$ (i.e. $\Omega(n)=k$ when $n=p^k$).
I believe $C_3(s)$ and $K_\Omega(s)$ defined in formulas (1) and (2) above can be analytically continued from $\Re(s)>1$ to $\Re(s)>0$ as follows
$$C_3(s)=\underset{N\to\infty}{\text{lim}}\left(-\sum\limits_{n=1}^N \phi(n)\, \frac{\zeta'}{\zeta}(n s))\right),\quad\Re(s)>0\tag{3}$$
$$K_\Omega(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N b(n)\, \log\zeta(n s)\right),\quad\Re(s)>0\tag{4}$$
where $\phi(n)$ is Euler's totient function and
$$b(n)=\frac{1}{n}\sum\limits_{d|n} d^2\, \mu\left(\frac{n}{d}\right)\tag{5}$$
Note that $b(n)\, n=\sum\limits_{d|n} d^2\, \mu\left(\frac{n}{d}\right)$ corresponds to OEIS Entry A007434 for the Jordan function $J_2(n)$ which is a generalization of Euler's totient function $\phi(n)$ and
$$\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N A007434(n)\, n^{-s}\right)=\frac{\zeta(s-2)}{\zeta(s)},\quad\Re(s)>3\tag{6}$$
whereas
$$\underset{\text{N}\to\infty}{\text{lim}}\left(\sum_{n=1}^N b(n)\, n^{-s}\right)=\frac{\zeta(s-1)}{\zeta(s+1)},\quad\Re(s)>2\tag{7}$$
and
$$\underset{\text{N}\to\infty}{\text{lim}}\left(\sum_{n=1}^N \phi(n)\, n^{-s}\right)=\frac{\zeta(s-1)}{\zeta(s)},\quad\Re(s)>2\tag{8}$$
I believe $C_3(s)$ and $K_\Omega(s)$ defined in formulas (1) and (2) above can also be evaluated as follows
$$\hat{C}_3(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=2}^N \frac{1_{n\in\mathbb{P}}\, \log(n)}{n^s+n^{-s}-2}\right),\quad|\Re(s)|>1\tag{9}$$
$$\hat{K}_\Omega(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=2}^N \frac{1_{n\in\mathbb{P}}}{n^s+n^{-s}-2}\right),\quad|\Re(s)|>1\tag{10}$$
for $\Re(s)>1$ which is illustrated in Figures (1) to (6) following my questions below where $1_{n\in\mathbb{P}}$ is the prime indicator function which returns the value $1$ if $n$ is a prime and zero otherwise.
Note formulas (9) and (10) above for $\hat{C}_3(s)$ and $\hat{K}_\Omega(s)$ converge for $\Re(s)<-1$ as well as $\Re(s)>1$ and evaluate to $\hat{C}_3(-s)$=$\hat{C}_3(s)$ and $\hat{K}_\Omega(-s)$=$\hat{K}_\Omega(s)$ for $|\Re(s)|>1$.
Question (1): Is there a name for functions such as $\hat{C}_3(s)$ and $\hat{K}_\Omega(s)$ defined in formulas (9) and (10) above which converge in the left and right half planes except for a vertical strip between the two?
Question (2): In light of the alternate representation of $C_3(s)$ and $K_\Omega(s)$ defined in formulas (1) and (2) above for $\Re(s)>1$ via $\hat{C}_3(s)$ and $\hat{K}_\Omega(s)$ defined in formulas (9) and (10) above, does it make sense to talk about the analytic continuation of $C_3(s)$ and $K_\Omega(s)$ defined in formula (3) and (4) above from $\Re(s)>0$ to $\Re(s)<0$ via the functional equations $C_3(-s)$=$C_3(s)$ and $K_\Omega(-s)$=$K_\Omega(s)$ even though they would be undefined along the imaginary axis where $\Re(s)=0$?
Question (3): Assuming the answer to question (2) above is no, does this imply $\hat{C}_3(s)$ and $\hat{K}_\Omega(s)$ defined in formulas (9) and (10) must be treated as different functions than $C_3(s)$ and $K_\Omega(s)$ defined in formulas (1) to (4) above in which case they might have an analytic continuation from $|\Re(s)|>1$ to the entire complex plane including the imaginary axis where $\Re(s)=0$ with the functional equations $\hat{C}_3(-s)$=$\hat{C}_3(s)$ and $\hat{K}_\Omega(-s)$=$\hat{K}_\Omega(s)$?
It's a bit unclear to me how analytic continuation and its uniqueness apply to the formulas in this question (see Initial discussion under the Wikipedia article on Analytic continuation) since $|\Re(s)<1|$ does not represent a connected domain and neither does $\Re(s)\ne 0$.
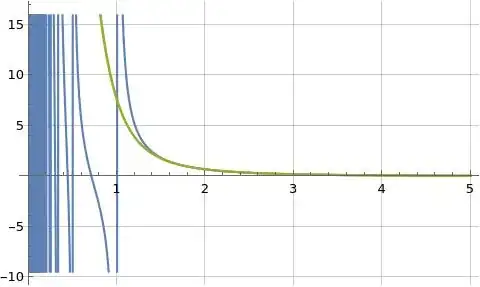
The following three figures illustrate formulas (1) and (3) for $C_3(s)$ above in orange and blue and formula (9) for $\hat{C}_3(s)$ above in green where formula (3) is evaluated at $K=100$ and formulas (1) and (9) are both evaluated at $K=1000$. Formula (3) for $C_3(s)$ is used as a reference function as I believe it converges more rapidly than the related Dirichlet series defined in formula (1) which is one of the reasons a lower evaluation limit is used for formula (3), and another reason is the terms of formula (3) take much longer to evaluate than the terms of formulas (1) and (9).
Figure (1): Illustration of formulas (1) and (3) for $C_3(s)$ (orange and blue) and formula (9) for $\hat{C}_3(s)$ (green) evaluated for real $s$
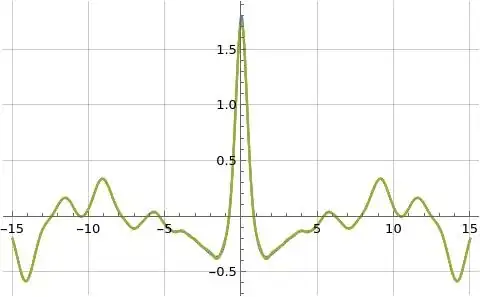
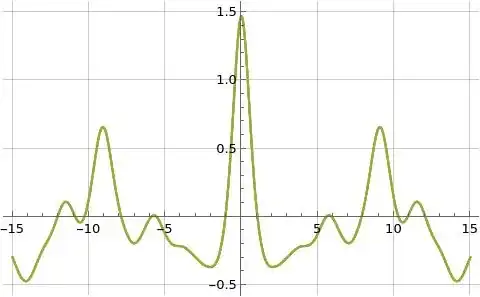
Figure (2): Illustration of real part of formulas (1) and (3) for $C_3(s)$ (orange and blue) and formula (9) for $\hat{C}_3(s)$ (green) evaluated along the line $s=\frac{3}{2}+i t$
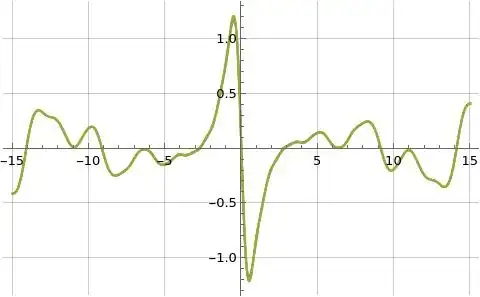
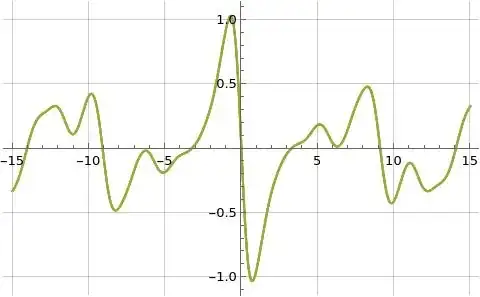
Figure (3): Illustration of imaginary part of formulas (1) and (3) for $C_3(s)$ (orange and blue) and formula (9) for $\hat{C}_3(s)$ (green) evaluated along the line $s=\frac{3}{2}+i t$
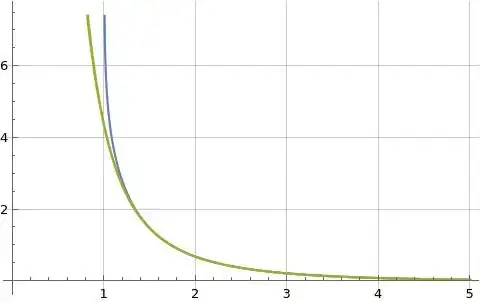
The following three figures illustrate formulas (2) and (4) for $K_\Omega(s)$ above in orange and blue and formula (10) for $\hat{K}_\Omega(s)$ above in green where formula (4) is evaluated at $K=100$ and formulas (2) and (10) are both evaluated at $K=1000$. Formula (4) for $K_\Omega(s)$ is used as a reference function as I believe it converges more rapidly than the related Dirichlet series defined in formula (2) which is one of the reasons a lower evaluation limit is used for formula (4), and another reason is the terms of formula (4) take much longer to evaluate than the terms of formulas (2) and (10).
Figure (4) below only illustrates formula (4) where it evaluates as strictly real which is for $s>1$ because Mathematica's evaluation of $\log\zeta(s)$ has an imaginary part for $0<s<1$ due to the branch cut of $\log(s)$ along the negative real axis.
Figure (4): Illustration of formulas (2) and (4) for $K_\Omega(s)$ (orange and blue) and formula (10) for $\hat{K}_\Omega(s)$ (green) evaluated for real $s$
Figure (5): Illustration of real part of formulas (2) and (4) for $K_\Omega(s)$ (orange and blue) and formula (10) for $\hat{K}_\Omega(s)$ (green) evaluated along the line $s=\frac{3}{2}+i t$
Figure (6): Illustration of imaginary part of formulas (2) and (4) for $K_\Omega(s)$ (orange and blue) and formula (10) for $\hat{K}_\Omega(s)$ (green) evaluated along the line $s=\frac{3}{2}+i t$