0

Consider the following two representations of $f(s)$

$$f(s)= \underset{K\to\infty}{\text{lim}}\left(\prod\limits_{k=1}^K \left(1-\frac{2}{\left.p_k\right.^s}\right)\right)\tag{1}$$

$$f(s)=\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=1}^N \frac{\mu(n)\ \sigma_0(n)}{n^s}\right)\tag{2}$$

where $p_k$ is the $k^{th}$ prime.

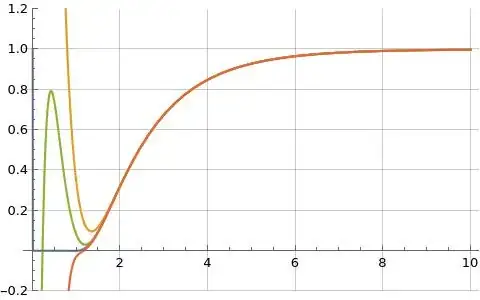
I believe formulas (1) and (2) above both converge for something like $\Re(s)\ge 1$, but formula (1) above also seems to converge for $s>0$ which is illustrated in Figure (1) below, however I don't believe formula (1) converges more generally for $\Re(s)>0$.

Question (1): What is the convergence of formulas (1) and (2) above? Is it atypical for a product representation to converge over a wider range of $s\in\mathbb{R}$ than it's associated Dirichlet series?

Question (2): Is there an analytic continuation of $f(s)$ for $s\in\mathbb{C}$ or at least for $\Re(s)>0$ that matches formula (1) above when evaluated for $0<s<1$?

Figure (1) below illustrates formula (1) for $f(s)$ evaluated at $K=1,000$ in blue and formula (2) for $f(s)$ evaluated at $N=100$, $N=1,000$, and $N=10,000$ in orange, green, and red respectively. Note formula (1) seems to converge for $s>0$ whereas formula (2) only seems to converge for $s\ge 1$.

Illustration of formula (1) (blue) and formula (2) (orange, green, and red) for f(s)

Figure (1): Illustration of formula (1) (blue) and formula (2) (orange, green and red) for $f(s)$

Note in Figure (1) above formula (1) for $f(s)$ shown in blue seems to evaluate somewhat analogous to a Cumulative Distribution Function (CDF) related to the primes when evaluated for $s>0$.

Question (3): Is there a closed-form representation of formula (1) above when evaluated for $s>0$, or does formula (1) correspond to some known CDF?

There are many other Dirichlet series related to the product representation $f(s)=\prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)$ defined in formula (1) above some of which are defined below. Several of the formulas below provide references to related OEIS entries. Note formula (4) below overlaps formulas (1) and (2) above.

$$\sum\limits_{n=1}^\infty \left(\sum\limits_{d|n} \mu(d) 2^{\nu(d)} \mu\left(\frac{n}{d}\right)\right) n^{-s}=\frac{1}{\zeta(s)} \prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\ \text{(see A326814)}\tag{3}$$

$$\sum\limits_{n=1}^\infty \mu(n)\, 2^{\nu (n)}\, n^{-s}=\prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\ \text{(see A226177)}\tag{4}$$

$$\sum\limits_{n=1}^\infty (-1)^{\nu (n)}\, n^{-s}=\zeta(s)\,\prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\ \text{(see A076479)}\tag{5}$$

$$\sum\limits_{n=1}^\infty \left(\sum\limits_{d|n} (-1)^{\nu (d)}\right) n^{-s}=\zeta(s)^2\,\prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\tag{6}$$

$$\sum\limits_{n=1}^\infty \left(\sum\limits_{d|n} \left(\left\{\begin{array}{cc} -1 & 4|d \\ 1 & \text{otherwise} \\ \end{array}\right.\right) (-1)^{\nu(d)} \mu\left(\frac{n}{d}\right)\right) n^{-s}=\left(\frac{2^{1-s}}{2^s-2}+1\right) \prod _{k=1}^{\infty } \left(1-2 \left(p_k\right){}^{-s}\right)\ \text{(see A306653)}\tag{7}$$

$$\sum\limits_{n=1}^\infty \left(\left\{\begin{array}{cc} -1 & 4|d \\ 1 & \text{otherwise} \\ \end{array}\right.\right) (-1)^{\nu(n)} n^{-s}=\left(\frac{2^{1-s}}{2^s-2}+1\right) \zeta(s) \prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\tag{8}$$

$$\sum\limits_{n=1}^\infty (-1)^{n+1} \left(\sum\limits_{d|n} (-1)^{\nu(d)}\right) n^{-s}=\left(\frac{2^{1-s}}{2^s-2}+1\right) \zeta(s)^2 \prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\ \text{(see A298826)}\tag{9}$$

$$-\sum\limits_{n=1}^\infty \mu(2 n)\, \sigma_0(n)\, n^{-s}=\frac{1}{1-2^{1-s}} \prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\tag{10}$$

$$\sum\limits_{n=1}^\infty (-1)^{n-1} (-1)^{\nu(n)} n^{-s}=\frac{\zeta(s)}{1-2^{1-s}} \prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\tag{11}$$

$$\sum_{n=1}^\infty \left(\sum\limits_{d|n} (-1)^{d-1} (-1)^{\nu(d)}\right) n^{-s}=\frac{\zeta(s)^2}{1-2^{1-s}} \prod\limits_{k=1}^\infty \left(1-2 \left(p_k\right){}^{-s}\right)\tag{12}$$

I believe the Dirichlet series and product representations in formulas (3) to (12) above are generally equivalent for $\Re(s)>1$. Based on a comment below, I believe the product representations generally diverge for $\Re(s)<1$, and at least in some cases the Dirichlet series converge for $\Re(s)>\frac{1}{2}$ assuming the Riemann hypothesis, but I'm not sure if any of the Dirichlet series above can be analytically extended beyond $\Re(s)>\frac{1}{2}$.

OEIS entry A298826 seems to imply the twin-prime conjecture is related to the evaluation of the Dirichlet series in formula (9) above at $s=1$, but I'm not sure if and how any of the other Dirichlet series defined above are also related to the twin-prime conjecture.

Steven Clark
  • 8,744
  • $\prod_p (1-2 p^{-s})$ converges for $\Re(s)\ge 1$ and not beyond (it diverges to $0$ on $(0,1)$ Under the RH $\sum\limits_{n=1}^\infty \frac{\mu(n)\ \sigma_0(n)}{n^s}$ converges for $\Re(s) >1/2$. It cannot converge for $\Re(s)>0$. – reuns Sep 10 '22 at 21:30
  • @reuns Interesting, that's not what I expected. When you say it cannot converge for $\Re(s)>0$, are you talking about the Dirichlet series or are you saying the Dirichlet series cannot be analytically extended beyond $\Re(s)>\frac{1}{2}$? – Steven Clark Sep 11 '22 at 00:06
  • @StevenClark That would be a different problem. However, it is known that it is impossible for $\sum_p p^{-s}$ to be extended beyong $\Re(s)\ge0$ because the imaginary axis is its natural boundary (consult Titchmarsh for a proof). – TravorLZH Sep 11 '22 at 10:45
  • @TravorLZH I'm aware of natural boundary of the analytic continuation $P(s)=\sum\limits_{n=1}^\infty\frac{\mu(n)}{n}, \log\zeta(n, s)$ of the prime zeta function $P(s)=\sum\limits_p \frac{1}{p^s}$. I believe the analytic continuation $K(s)=\sum\limits_{n=1}^\infty\frac{\phi(n)}{n},\log\zeta(n, s)$ of the prime-power zeta function $K(s)=\sum\limits_{p^k}\frac{1}{\left(p^k\right)^s}$ has the same natural boundary, and also see my question at https://math.stackexchange.com/q/4470369 for a couple of other related functions. – Steven Clark Sep 11 '22 at 16:29
  • @TravorLZH I'm wondering if the analytic continuation of $f(s)=\sum\limits_{n=1}^\infty \frac{\mu(n)\ \sigma_0(n)}{n^s}$ has poles at the zeros of $\zeta(s)$ (which seems to be suggested by some of my evaluations and the comment above by user reuns), and if this analytic continuation is valid for all $s\in\mathbb{C}$ or perhaps only $\Re(s)>0$ similar to the prime zeta function $P(s)$. – Steven Clark Sep 11 '22 at 16:30
  • @StevenClark It can be shown that $f(s)=g(s)\zeta^2(s)$ where $g(s)$ is some Dirichlet series that converges absolutely on $\Re(s)>1/2$. The difficulty here is that we don't know how to extend the domain of $g(s)$. – TravorLZH Sep 12 '22 at 09:52

0 Answers0