Characterize open sets of this quotient topology.

Question

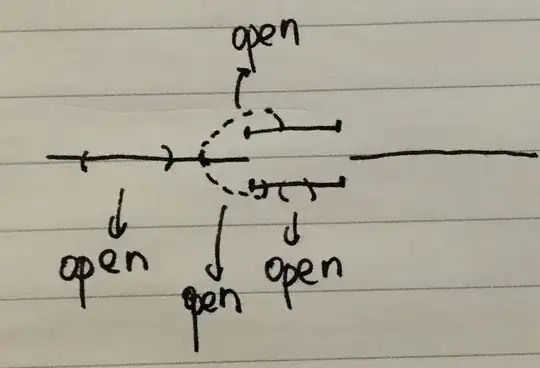
Let $X$ the quotient space obtained from $\mathbb{R}\times\{0,1\}$ identifying $(x,0)\sim(x,1)$ if $|x|>1$. Which are the open sets of this quotient topology?

First, I've made the next drawing to understand the identification going on here:

Then I constructed the relation of equivalence as follows: $$\text{Relation of Equivalence:}\begin{cases} (x,0)\sim (x,1) &\text{ if } |x|>1\\ (x,1)\sim (x,0) &\text{ if } |x|>1\\ (x,y)\sim (x,y) &\text{ if } |x|\leq 1 \end{cases}$$ In order to characterize open sets, let $q:\mathbb{R}\times\{0,1\}\to X$ a quotient map. This is where I'm getting stuck, I propose the following map: $$q(x,y)=\begin{cases} (x,0)& \text{ if } |x|>1,~\forall y\in\{0,1\}\\ (x,y)& \text{ if } |x|\leq 1,~\forall y\in\{0,1\} \end{cases}$$ I'm not sure how to construct the partition needed with this $~$, or if this map $q$ is well defined, and who are open sets.

I know the definition: $U$ is an open set of $(X,\tau_{X_\sim})\iff$ $q^{-1}(U)$ is open in $(\tau_p,\mathbb{R}\times\{0,1\})$.

Is the reasoning correct? How can I characterize open sets? Should I do them with cases?

Answer 1

Here the elements of your quotient space $X$ should be the set of all equivalent classes of your equivalence relation, denote the equivalent class of $(x, y)$ as $[(x, y)]$. Then we know that $[(x, 1)] = [(x, 0)] = \{(x, 0), (x, 1)\}$ for all $|x| > 1$ and $[(x, 1)] = \{(x, 1)\}$, $[(x, 0)] = \{(x, 0)\}$ for all $|x| \leq 1$.

Write $X$ out explicitly(since the elements as equivalence classes are sets, it's quite tedious):

$$ \begin{align} X =& \{[(x, y)]|(x, y) \in \Bbb{R} \times \{0, 1\}\} \\ =&\{\{(x, 1), (x, 0)\}|x \in \Bbb{R} ,|x| > 1\} \\&\cup\{\{(x, 0)\}|x\in\Bbb{R}, |x|\leq 1\}\} \\ &\cup\{\{(x, 1)\}|x\in\Bbb{R}, |x|\leq1\}\} \end{align} $$

the quotient map should be:

$$ \begin{align} q(x, y) &= [(x, y)] \\ &= \begin{cases} \{\{(x, 1), (x, 0)\}\}, & \text{if}\ |x|>1 \\ \{\{(x, 0)\}\}, & \text{if}\ |x| \leq 1, y = 0 \\ \{\{(x, 1)\}\}& \text{if}\ |x| \leq 1, y = 1 \end{cases} \end{align} $$

Here in fact $X$ is quite like the space line with two origins, or branching line, see the question The Line with two origins too. Maybe you can call your space as "line with two segment". Its open sets are any open sets in the open sets (and union of them) in the two half lines and the two segments, including their endpoints. and beware that the two half lines contain no endpoints but each of the two segment contains two endpoints. So the open sets in the two segments containing the "half-open half-closed" intervals.

Denote the open set of $\Bbb{R}\times\{0,1\}$ as $\tau$, and the open set of $X$ as $\tau_{X}$. Then as you said, $ U \in \tau_X \Leftrightarrow q^{-1}(U) \in \tau.$ $U$ can be written as $$ U = \cup_{x \in A}\{\{(x, 1),(x, 0)\}\} \cup_{x \in B} \{\{(x,0)\}\} \cup_{x \in C} \{\{(x,1)\}\} $$ , where $A \subset \{x \in \Bbb{R}|~|x|>1\}$, $B, C \subset \{x \in \Bbb{R}|~|x|\leq1\}$. Then

$$q^{-1}(U)=A\times\{1\}\cup\{A\}\times\{0\}\cup B\times \{0\} \cup C\times \ \{1\}.$$

It's open if and only if $A\cup B$ and $A\cup C$ are open in $\Bbb{R}$. So it concides with our intuitive description.