Prove that the null set is a subset of a set $A$.

Question

Prove that $\; \emptyset \subseteq A$.

The statement seems obvious to me, but how do I prove it?

My instructor said to prove that the statement is vacuously true, but I'm not sure what that means.

Answer 1

Recall that to prove any set $X$ is a subset of another set $Y$, we must prove the following implication:

$$\text{For all}\; x \in X,\,\; {\bf if}\;\, x \in X,\; {\bf then}\;\, x \in Y.$$

More formally, that's $$X\subseteq Y \;\;\text{if and only if}\;\;\forall x\in X,\; \left(x\in X\implies x\in Y\right)\tag{1}$$

Now, an implication (aka, a conditional statement) is true any time the antecedent of the conditional (which is the statement to the left of the implication sign $\implies$) is false. (When this happens, the implication is said to be vacuously true). Furthermore, an implication is true any time the statement to the right of the implication sign is true.

An implication is false if and only if it happens to be the case that the left-hand side of the implication is true, but (and) the right-hand side is false. (I'll include the truth-table for the conditional connective below (compliments of W|A) as a refresher:

$\qquad\qquad\qquad\qquad$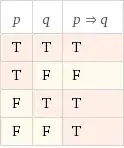

Now, the following assertion happens to be vacuously true for all sets $X$:

$$\text{Let X be any set, and $x$ be any element. Then}\;\;x\in \varnothing \implies x\in X\tag{2}$$

This implication is vacuously true because $x\in \varnothing$ never happens to be the case: there is no element $x \in \varnothing$, by the definition of $\varnothing$, so it cannot possibly be the case that there exists an $x \in \varnothing$ and such that $x \notin X$. So we know simply by virtue of this fact that the entire implication is thereby (vacuously) true.

Now, $(2)$ is exactly what we wanted to prove, and we've shown it is vacuously true. That is: For all sets $X$ and any element $x$, if $x\in \varnothing$, then $x \in X$. Therefore, $\varnothing \subseteq X$, for all sets $X$.

Answer 2

amWhy’s answer explains the technical details, but you may still find the intuition behind them a bit murky. Perhaps the easiest way to think about it is to ask yourself what it means to say that a set $X$ is not a subset of a set $Y$: there is some object that is in $X$ but not in $Y$. Thus, to show that $\varnothing$ is not a subsets of $A$, we must be able to find some object $x$ such that $x\in\varnothing$, but $x\notin A$. Of course we can’t do this: we can’t even find an $x\in\varnothing$, never mind whether $x\in A$ or not! Thus, $\varnothing\subseteq A$ cannot be false and must therefore be true.

We sometimes express this by saying that there is no object that witnesses the statement $\varnothing\nsubseteq A$, meaning that there is no object $x$ such that $x\in\varnothing$ and $x\notin A$. In this terminology, if $P$ is the set of prime numbers, and $A$ is the set of odd numbers, then the number $2$ witnesses the statement $P\nsubseteq A$.

Answer 3

Rewrite the statement in first order logic: $(\forall x\in \varnothing)(x\in A)$. Note that this formula is just short for $$\forall x(x\in \varnothing\implies x\in A)$$

Answer 4

Formally, you are asked to prove $$\varnothing \subseteq A$$ for every set $A$.

An approach I always try to use for this type of problem is to translate set theory to logic by expanding definitions, and then simplify. In this case, we see that for every set $A$ \begin{align} & \varnothing \subseteq A \\ \equiv & \;\;\;\;\;\text{"definition of $\;\subseteq\;$"} \\ & \langle \forall x :: x \in \varnothing \Rightarrow x \in A \rangle \\ \equiv & \;\;\;\;\;\text{"definition of $\;\varnothing\;$: no $\;x\;$ is an element of $\varnothing$"} \\ & \langle \forall x :: \textrm{false} \Rightarrow x \in A \rangle \\ (*) \equiv & \;\;\;\;\;\text{"logic: simplify: $\;\textrm{false}\;$ implies everything, see below"} \\ & \langle \forall x :: \textrm{true} \rangle \\ \equiv & \;\;\;\;\;\text{"logic: simplify, allowed because $\;\textrm{true}\;$ does not contain $\;x\;$"} \\ & \textrm{true} \\ \end{align} which completes the proof.

If you want more detail on step $(*)$, then observe that for any boolean expression $P$ \begin{align} & \textrm{false} \Rightarrow P \\ \equiv & \;\;\;\;\;\text{"logic: expand $\;\Rightarrow\;$"} \\ & \lnot\textrm{false} \lor P \\ \equiv & \;\;\;\;\;\text{"logic: simplify left hand side"} \\ & \textrm{true} \lor P \\ \equiv & \;\;\;\;\;\text{"logic: simplify"} \\ & \textrm{true} \\ \end{align}

Answer 5

Every frog in your magnetron is blue! True or not? Yes it is true since you cannot find any frog in your magnetron that is not blue. Even stronger: you cannot even find any frog there at all, so certainly not one that is not blue.

Proven is now (vacuously) that the frogs in your magnetron (empty) all belong to the set of blue objects.

Caution: This is only valid if you have no frogs in your magnetron.