Here is a partial inspiration for this question:
and
this is the same question, but has no current answer and only asks for a proof for a non-algebraic solution whereas I ask about a true solution.
I know it is not traditional to ask 2 questions, but I cannot choose which equation to solve, so I will solve very simple first order nonlinear differential equations:
$$y’=x^y\text{ and }y’=y^x$$
Here are the solutions:
$$y+c=\int y^x dx,y+c=\int x^y dx$$
There is also no way I can use the Frobenius method as the serie solution method.
Let’s try to separate the variables ignoring restrictions for now:
$$y’=x^y\implies \ln(y’)=y\ln(x)\implies \log_x(y’)=y\implies y’^\frac1y=x\mathop\implies^{\frac d{dx}}1=\frac{y’(x)^{\frac1y-1}(yy’’-y’^2\ln(y’))}{y^2} $$$$y’=y^x\implies y’^\frac1 x=y\implies \log_y(y’)=\frac{\ln(y’)}{\ln(y)} \mathop\implies^{\frac d{dx}} 1=\frac{y’’}{\ln(y)y’}-\frac{\ln(y’)y’}{\ln^2(y)y}$$
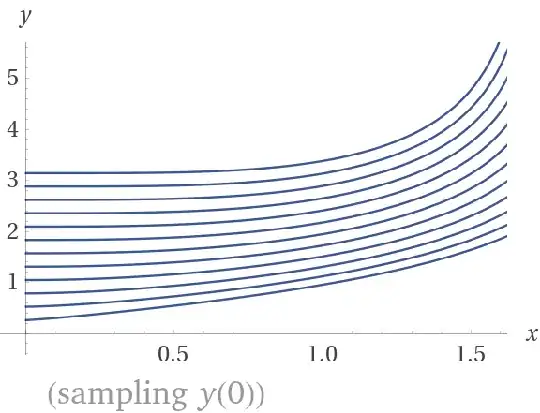
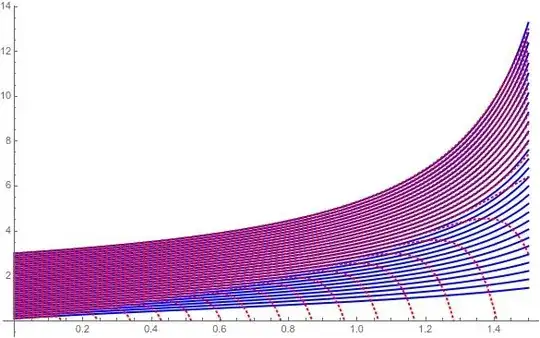
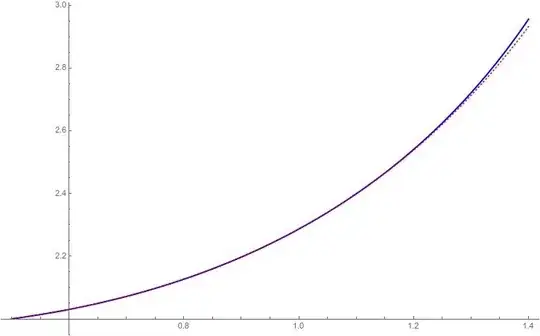
Here is the solution set family and differential curves for $y’=x^y$:
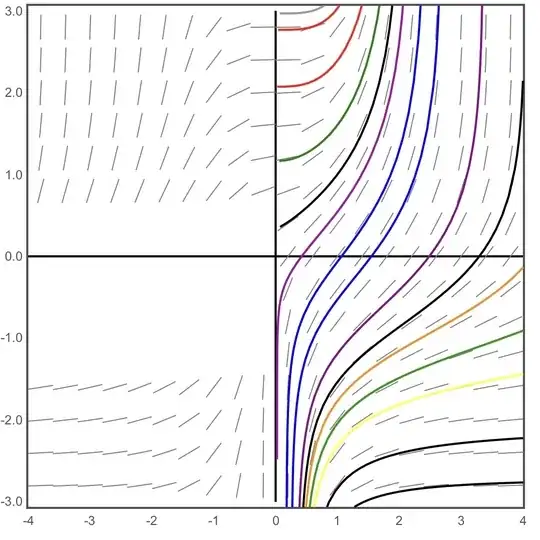
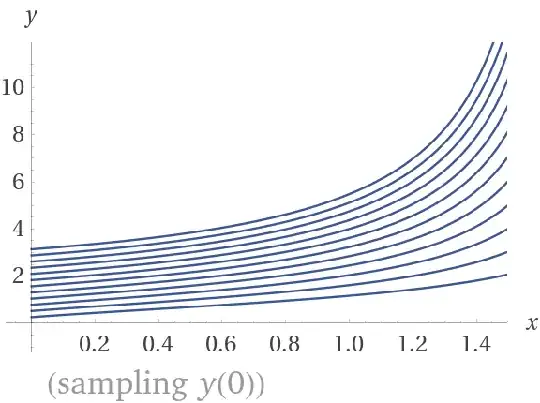
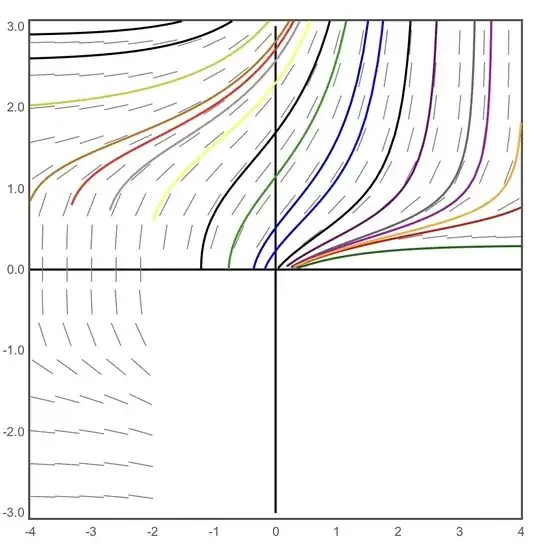
Here is the solution set family for $y’=y^x$:
 How do I solve for $y’=x^y$ and $y’=y^x$ for $y$ explicitly? Any series solution is appreciated. If there is a closed form, then please also write it even though it seems unlikely.
How do I solve for $y’=x^y$ and $y’=y^x$ for $y$ explicitly? Any series solution is appreciated. If there is a closed form, then please also write it even though it seems unlikely.
Here is some progress on $y’=x^y$ using the fact that $$x^{\sum\limits_{n\ge0} A_n}=\prod_{n\ge0} x^{A_n}:$$
$$y=\sum_{n\ge 0} a_n x^n\implies \sum_{n\ge1} a_n nx^{n-1}-\prod_{n\ge0} x^{a_n x^n} =0\implies a_1 +2 a_2 x+3 a_3x^2+…-x^{a_0}x^{a_1x}x^{a_2 x^2}\cdot …=0$$
If we were to assume that $\{a_n\}=0$, then this would not work as we have the coefficients in the exponent.
For the other differential equation, one can find the following power series using an experimental infinite Multinomial Theorem. I will also use the aforementioned Pi Product notation and factorial definition of the multinational for a representation in terms of more common functions. $n_m$ is just the mth index with the condition that the sum of all infinite number of indices is $x$. There may be a typo:
$$y’=y^x,y=\sum_{n\ge0} a_n x^n\implies\sum_{n\ge1} a_n nx^{n-1}=\left(\sum_{n\ge0}a_n x^n\right)^x\implies \sum_{n\ge1} a_n nx^{n-1}-\sum_{\sum\limits_{m\ge1} n_m=x}\frac{x!\prod\limits_{t\ge0} a_t^{n_m}x^{tn_m}}{\prod\limits_{k\ge 1}n_m!}=0$$
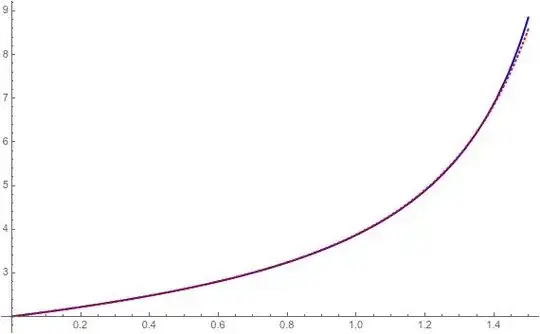
Here is an attempt to put $y’=x^y$ into a more manageable form using a similar method as @Cesareo’s keeping restrictions in mind. This is the corrected answer:
$$y’=x^y\implies y’’=x^{y-1}(x\ln(x)y’+y)\implies y’=x^y=\frac{xy’’}{x\ln(x)y’+y}\implies xy’’=x\ln(x)y’^2+yy’\implies\boxed{ xy’’-x\ln(x)y’^2-yy’=0}$$
which has no apparent solution so ho would I solve $$xy’’-x\ln(x)y’^2-yy’=0$$
I can think of a power series which may or may not need $2$ different indices:
$$\sum_{n=2}^\infty a_n n(n-1)x^{n-1}-x\ln(x)\sum_{n=1}^\infty a_n nx^{n-1}\sum_{n=1}^\infty a_n nx^{n-1}-\sum_{n=0}^\infty a_n x^n \sum_{n=1}^\infty a_n nx^{n-1}=0$$
We are so close to solving, so do you have any ideas? Please correct me and give me feedback!