ODE: $y''y+ax+by+c=0,y=k\pm\sqrt2\int\sqrt{a\int\ln(y)dx-(ax+c)\,\ln(y)-by+K}dx,\int\frac{dy}{\sqrt{K-(ax+c)\,\ln(y)+a\int\ln(y)dx-by}}=k\pm\sqrt2x$

Question

Imagine we had a differential equation like: $$y’’-\frac xy=0$$

Now let’s standardize the signs. Note we do not need a constant for the first term because of the zero product property. We can generalize any way we want, but this way of adding constants will generalize linearly and intuitively:

$$y’’+\frac {ax+c}{y}+b=0\implies y’’y+ax+by+c=0\implies y=y(a,b,c;x)\ne 0$$

where a,b,c are any constants

Notice that we can then do:

$$y’’+a\frac {x+\frac ca}{y}+b=0\implies y’’y+a\left(x+\frac ca\right)+by=0$$

It can be shown that an implicit solution for $y=y(0,b,c;x)$ is the function $y(x)$ which satisfies the following functional integral equation. Be careful with the squared terms when solving here:

$$y’’y+by+c=0\implies\left(\int_1^{y(x)}\frac{dt}{\sqrt{c_1-2(bt+c\ln(t)))}}\right)^2=(x+c_2)^2$$

This might remind you of an inverse gamma-type function which I did not see coming. Another nice thing is a closed form for $y(0,0,c;x)$ which uses the Inverse Error function:

$$y’’y+c=0\implies y(x)=e^{\frac{c_1-2c\left(\operatorname{erf}^{-1}\left(\pm \sqrt{\frac 2\pi}\sqrt{ce^{-\frac{c_1}{c}}(x+c_2)^2}\right)\right)^2}{2c}} \implies \left(\int_1^{y(x)}\frac{dt}{\sqrt{c_1-2c\ln(t))}}\right)^2=(x+c_2)^2$$

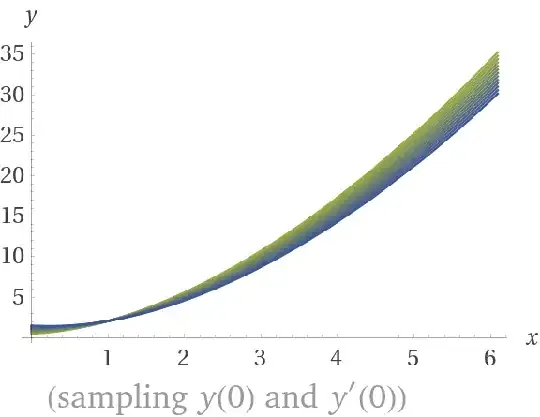
Here is what the sample solution family for $y’’y+x+y+1=0\ $looks like:

Here is what the sample solution family for $y’’y-x-y-1=0\ $ looks like:

Related problems:

Approach Zero Search Results

This almost looks like the Airy Differential Equation, but it is not related:

$$y’’-xy=0\implies y=\operatorname{Ai}(x)+i\operatorname {Bi}(x)$$

Unfortunately, we cannot use the Principle of Superposition to find a more general solution as the equation is nonlinear. @Eli showed that the following is a particular solution:

$$y=-\frac{ax+c}b\ne 0\implies -\frac{ax+c}b \frac{d^2}{dx^2} \frac{-ax-c}b +ax-b\frac{ax+b}b +c=0+ax-ax-c+c=0$$

The problem is that this is not the general solution. One attempt at finding such a general solution will use our aforementioned a=0 using a Generalized Puisex Series, with machine help, at t=0, but the convergence may be a problem. I have listed out a few of many known terms:

$$y’’y+by+c=0\implies\left(\int_1^{y(x)}\frac{dt}{\sqrt{k-2(bt+c\ln(t)))}}\right)^2=(x+c_2)^2\implies \int_1^{y(x)}\frac{dt}{\sqrt{k-2(bt+c\ln(t))}}=\int_1^{y(x)}\left(\frac 1{\sqrt{k - 2 c \ln(t)}}+ \frac{b t}{(k - 2 c \ln(t))^\frac32} + \frac{3 b^2 t^2}{(2 (k - 2 c \ln(t))^\frac52)} +O\left(t^3\right)\right) $$

Then one may use an inversion theorem to find the inverse and find $y(x)$ with correct convergence.

My question is how to either find a closed form for $y(x)=y(a,b,c;x)$ or a general series representation for the general case without any initial values. Please do not give any implicit solutions as the goal is to find $y(x)$. You can even use an inversion theorem like the Lagrange Inversion Theorem. Please correct me and give me feedback!

Here is a general integral solution for which the main integral we need to put in terms of x. Here is a reference problem for the technique used by @Ron Gordon to solve the general solution and somehow integrate a general $y’y’’$:

Solution to Differential Equation: $y'' = \frac{c_1}{y} - \frac{c_2}{y^2} $.

$$y’’y+ax+by+c=0\mathop \implies^{y\ne0} y’’+a\frac x{y’}+b+ \frac cy=0\implies -y’’y’= a\frac {x y’}{y}+by’+ c\frac {y’}y$$

Now we integrate and use the referenced integration technique along with Logarithmic Differentiation. One also uses Integration by Parts of x and $\frac {y’}{y}$:

$$ \int -y’’y’dx= a\int \frac {x y’}{y}dx+b\int y’dx+ c\int \frac {y’}y dx\implies c_1-\frac{y’^{\,2}}2=ax\,\ln(y)-\int \ln(y) dx+c_2+by+c_3+c\,\ln(y)+c_4\implies y’^{\,2}=-2ax\,\ln(y)+2a\int \ln(y)dx-2by-2c\,\ln(y)+c_1\implies y’=\pm\sqrt{c_1 -2ax\,\ln(y)+2a\int \ln(y)dx-2by-2c\,\ln(y)} \implies y=c_2\pm \sqrt 2\int\sqrt{a\int \ln(y)dx -ax\,\ln(y)-by-c\,\ln(y)+c_1} dx$$

Here is another way to solve:

$$\frac{y’}{\sqrt{c_1 -2ax\,\ln(y)+2a\int \ln(y)dx-2by-2c\,\ln(y)} }=\pm1\implies \int \frac{\frac{dy}{dx}}{\sqrt{c_1 -2ax\,\ln(y)+2\int \ln(y)dx-2by-2c\,\ln(y)}}dx=\pm\int dx \implies \int \frac{dy}{\sqrt{c_1 -2ax\,\ln(y)+2a\int \ln(y)dx-2by-2c\,\ln(y)}}=c_2\pm x\implies \int \frac{dy}{\sqrt{c_1 -ax\,\ln(y)+a\int \ln(y)dx-by-c\,\ln(y)}}=c_2\pm \sqrt2 x$$

This is where I got stuck. If we could integrate, by substitution in terms of x maybe, with a series expansion and use a series reversion, then it should output $y(x)$ explicitly.

Answer 1

I present to you 2 solutions. The first solves your ODE for the $b=0$ case by quadrature. The second is a solution via the power series method, which it seems like you'd be more interested in.

$\rule{170pt}{1pt}$

For $b=0$, the equation reduces to an Emden-Fowler equation, which can be transformed to an Abel equation of the second kind. Letting $y=-(ax+c)^{3/2}u/2$, and $ax+c=e^t$ brings the equation to an autonomous one, \begin{align} \ddot u=\dot u+\frac{3}{16}u+\frac{1}{a^2}\frac{1}{u}=0. \end{align} Now taking $\dot u=p(u)$, $\ddot u=pp'$ brings the equation to \begin{align} pp'=p+\frac{3}{16}u+\frac{1}{a^2}\frac{1}{u}. \end{align} This unfortunately does not fall under the Abel equations with simple solutions category. I'll copy the solution from "Exact analytic solutions of the Abel, Emden–Fowler and generalized Emden–Fowler nonlinear ODE" by Dimitrios E. Panayotounakosa and Dimitrios Kravvaritis without copying the method (it requires you to pay to view it). \begin{align} &p(u)=\frac{1}{2}(u+2\lambda)\left(\bar N(u)+\frac{1}{3}\right),\\ &G(\bar \xi)=\frac{e^{-\bar \xi}}{16}\frac{[(\bar \xi\sin(\bar \xi)\mathrm{ci}(\bar \xi)+\cos(\bar\xi)^2][4\bar \xi\mathrm{ci}(\bar\xi)+\cos(\bar \xi)]}{(\bar \xi \mathrm{ci}(\bar \xi))^3},\\ &\mathrm{ci}(\bar\xi)=-\int_{\bar\xi}^\infty\frac{\cos(s)}{s}\mathrm ds,\quad \bar\xi=\ln|u+2\lambda|,\\ &\left(\bar N(u)+\frac{4}{3}\right)^2-1=8\int\left[\frac{G(u)}{(u+2\lambda)^2}+\frac{1}{(u+2\lambda)^2}\left(\frac{3}{16}u+\frac{1}{a^2}\frac{1}{u}\right)\right]\mathrm du, \end{align}

where $\lambda$ is an integration constant. Here is a paper I'd consider a 'proof by graphing' for the solution. $u(t)$ is then given by \begin{align} 2\int \frac{\mathrm du}{(u+2\lambda)(\bar N(u)+1/3)}=t+\lambda_2, \end{align} and then $y(x)$ is implicitely given by \begin{align} \ln|ax+c|+\lambda_2=2\int \frac{\mathrm du}{(u+2\lambda)(\bar N(u)+1/3)},\quad u=\frac{-2y}{(ax+c)^{3/2}}. \end{align}

An implicit solution? Yes. A useful solution for your needs? I doubt it. Just maybe if you go through the dirty work of finding $\bar N(u)$ the integral turns out possible.

$\rule{170pt}{1pt}$

With $b\neq0$, it is similar to an Emden-Fowler equation, but does not succumb to the same trick to make it autonomous.

First, we can eliminate all three constants from your equation. Taking $y=a^2u/b$ and $ax+c=a^2\xi/b^2$, \begin{align} uu''+u+\xi=0. \end{align} I can't find an analytical solution or come up with one myself, so I'll use a power series solution. Assuming a power series solution of the form \begin{align} u(\xi)=\sum_{n\geq 0}c_n\xi^n,\quad u(\xi)''=\sum_{n\geq 0}(n+2)(n+1)c_{n+2}\xi^{n}. \end{align} The product $uu''$ can be found using the Cauchy product \begin{align} \left(\sum_{i\geq0}a_ix^i\right)\left(\sum_{j\geq0}b_ix^i\right)=\sum_{k\geq0}c_kx^k,\quad \text{where}\quad c_k=\sum_{l=0}^{k}a_lb_{k-l}. \end{align} So \begin{align} uu''=\sum_{n\geq0}b_n\xi^n,\quad \text{where}\quad b_n=\sum_{m=0}^n(m+1)(m+2)c_{2+m}c_{n-m}. \end{align} Substituting into the ODE gives that \begin{align} \sum_{n\geq0}(b_n+c_n)\xi^n+\xi=0. \end{align} For $n=0$: \begin{align} c_0(2c_2+1)=0. \end{align} The case of $c_0=0$ corresponds to the particular solution $u(\xi)=-\xi$. You can check that the rest of the coefficients turn out to be zero for this case.

Edit:

The coefficients are not that difficult to solve for, if you don't make mistakes! I've edited in the correct solution, and I've checked it in Desmos in the same manner that you have.

So for the other case we take \begin{align} c_2=-1/2. \end{align} Then the equation of recurrence becomes \begin{align} \xi+\sum_{n\geq0}\left(\sum_{m=1}^n (m+2)(m+1)c_{2+m}c_{n-m}\right)\xi^n=0. \end{align} Now correctly calculating the coefficients gives \begin{align} &n=1: 6c_3c_0=-1\\ &n=2: 6c_3c_1+12c_4c_0=0\\ &n=3: 6c_3c_2+12c_4c_1+20c_5c_0=0\\ &n=4: 6c_3^2+12c_4c_2+20c_5c_1+30c_6c_0=0\\ &n=5: 6c_3c_4+12c_4c_3+20c_5c_2+30c_6c_1+42c_7c_0=0. \end{align} Which has $c_0$ and $c_1$ as unknown quantities, corresponding to $c_0=u(0)$ and $c_1=u'(0)$, which makes much more sense than what I was touting before. Solving for some coefficients \begin{align} c_0&=u_0\\ c_1&=u'_0\\ c_2&=-1/2\\ c_3&=\frac{-1}{6c_0}\\ c_4&=\frac{-1}{2c_0}c_3c_1\\ c_5&=\frac{-1}{10c_0}(3c_3c_2+6c_4c_1) \end{align}

Finding an equation for $c_n$ is a matter of spotting patterns and guessing a few times, \begin{align} c_n=\frac{-1}{n(n+1)c_0}\sum_{m=4}^n(m-2)(m-1)c_{m-1}c_{n-m+1},\quad n\geq4 \end{align}

So the solution is given by \begin{align} u(\xi)=\sum_{n\geq0}c_n\xi^n, \end{align} where the coefficients are given by \begin{align} c_0&=u_0,\quad c_1=u'_0,\quad c_2=-1/2, \quad c_3=-1/(6c_0), \\c_n&=\frac{-1}{n(n+1)c_0}\sum_{m=4}^n(m-2)(m-1)c_{m-1}c_{n-m+1},\quad n\geq4. \end{align}

And in terms of $y(x)$: \begin{align} y(x)=\sum_{n\geq0}c_n\frac{b^{2n-1}}{a^{2n-2}}(ax+c)^n. \end{align}

Here I've input up to the 7th coefficient to check in Desmos.