6

I am trying to plot the standard bounds of simple Brownian motion (implemented as a Wiener process), but I have found some difficulties when drawing the typical equations:

  1. When trying to plot the bound given by the Law of the iterated logarithm: $ f_1(t) = \sqrt{2t\log(\log(t))}$, it fails to work at $t = [0 ; 1]$, because $\log(t) < 0$ so $\log(\log(t))$ is undefined.
  2. Then, I tried to fix it leting $ f_2(t) = \sqrt{2t\log(\log(t+1))}$, but again gives problems because it becomes "imaginary" due the square root of $\log(\log(t+1))<0$ on $t = [0 ; 1]$.
  3. So I tried again using $ f_3(t) = \sqrt{2t\log(\log(t+1)+1)}$ as the bound defined by the Law of the iterated logarithm, and it works (is well defined, and when $t \rightarrow \infty $ should reach a "similar" limit than the first attempts). Unfortunately, when plotted against many realizations of the Brownian paths, the bound is overpassed too many times at the start to be a good "tight" bound (it's "too tight").
  4. So, I tried another bound shown in the Wiener processes' Wikipedia named as "Modulus of Continuity", $f_4(t)=\sqrt{2t\log(\log(1/t))}$, which also have the "logarithm" problems as previous attempts for $t = [0 ; 1]$ (fixables), but it shows to be imaginary for almost all the domain $t > 0$. Not too promising (even when works good for valued near zero), but since it is also proportional to the first attempts (because $\log(1/t) = - \log(t)$), I tried using the absolute value of the adapted function for the "Modulus of Continuity" as the envelope-bound: $$f(t)_\pm=\pm\sqrt{2t\sqrt{\pi^2+{\log(1+\log(1+t))}^2}}$$ Which works really good as a tight bound for the Brownian realizations. Also at the beginning their behavior $\propto \sqrt{2t\pi}$ remembers me the bounds for standard 1D random walk which is $\sqrt{2t/\pi}$.

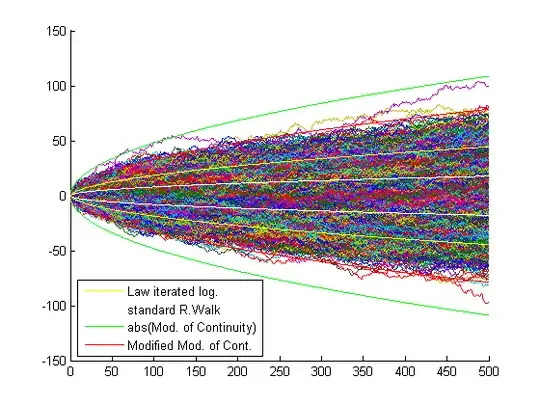
Example of tested bounds and Brownian realizations: https://i.sstatic.net/c6GQl.png

envelope behavior

The proposed bounds $f(t)_\pm$ are in green.

The red one is just a modification of the green one: $g(t)_\pm=\pm\sqrt{t\sqrt{\pi^2+{\log(1+\log(1+t))}^2}}$ which fits tight as an envelope of the shaded area. Both quite wider than the clasic one sigma deviation of a nornalized Brownian path ($\sigma=1$) which should be proportional to $\sqrt{t}$.

Actually it works so good, that I don't know if it is just a coincidence (maybe I made a mistake when defining the Brownian paths), but I don't found this bound in any website, so if right, it could be useful for everybody so I left it here, but certainly, I don't have the ability to probe anything related to it:

  1. If it is "mathematically" right? (such as the "real" form of the law of the iterated logarithm).
  2. If it is "tight" as an "almost-sure" true limit? (such something outside by a value $\epsilon \to 0$ don't going to be surpassed almost surely infinitely many times, but something inside will do).
  3. If it is going to be surpassed infinitely many times or not? (i It is really a frontier or not?)
  4. It is a "better" metric for/than the Law of the Iterated Logarithm?
  5. It is a "better" metric for/than the Modulus of Continuity?
  6. To which percentile these bounds are corresponding?, etc... (I tried to fit it in a gaussian distribution but it don't fit a constant-term deviation).

I hope you can help to tell me if is "mathematically" the "right envelope function, or just a mistake that has a beauty plot.

I left the code so you can play with it, is specially better at the first values (as it was mentioned, standard metrics fails here near zero).

Beforehand, thanks you very much.

The Matlab code I use:

length = 500;
N = 10000;
white_noise = wgn(length-1,N,0);
simple_brownian = zeros(length,N);
t = 0:1:(length-1);

%Wiener brownian vectors starting at zero
for m = 1:1:N
   simple_brownian(2:1:length,m) = cumsum(white_noise(:,m));
end


% Law of iterated logarithm (modif)
envp = sqrt(2.t.(log(1+log(1+t))));
envm = -envp;


% Proposed bounds
envp2 = sqrt(2.t.sqrt(pi^2+log(log(t+1)+1)).^2);
envm2 = -sqrt(2.t.sqrt(pi^2+log(log(t+1)+1)).^2);


figure(1), hold on,
plot(t,envp,'y',t,envm2,'g',t,envp2,'g',t,envm,'y'),
legend('Law iterated log.','Proposed bounds'),
plot(t,simple_brownian),
plot(t,envp,'y',t,envm2,'g',t,envp2,'g',t,envm,'y'),
hold off;

Added later

About point (5), commenting something mentioned in the comments: as $t\to \infty$ the Law of the Iterated Logarithm such as $f_{\pm}(t)$ will behave similar in the sense their fraction $\lim_{t\to \infty} \frac{f_\pm(t)}{\text{LIL}(t)}\to 1$ as can be seen in Wolfram-Alpha.

I think since the Modulus of continuity kind of show how much could change at max some function (as a kind-of-derivative when differentiation is undefined), it should fit the envelope I am looking for.

After some trials I think the found bound $f_{\pm}(t)$ could be improved just adjusting by just one displacement the mentioned Modulus of continuity of the Wiener process as: $$h(t)_\pm=\left|\sqrt{2t\log\left(\log\left(\frac{1}{t\color{red}{+1}}\right)\right)}\right|=\pm\sqrt{2t\sqrt{\pi^2+{\log(\log(1+t))}^2}}$$

But also, the classic LIL could be improved as:

$$k(t)_\pm = \pm\sqrt{2t\log(\log(t\color{red}{+e}))}$$

So for me is not clear at all which one is fulfilling being the "real envelope" of a wiener process and behaving as a LIL should do: as example $k_\pm(t)$ behaves more similar to $g_\pm(t)$ than it do to $h_\pm(t)$ (this is why, based on the plots, I think is $h_\pm(t)$ the better one).

Also, since at the beginning $h_\pm(t)$ behaves similar to $h_\pm(t) \sim \sqrt{2\pi t}$, neither is clear for me that if the standard deviation of a Brownian motion is $\sigma = \sqrt{t}$, then how should be interpreted this envelope corresponding to a standard deviation of $\sqrt{2\pi}\sigma$.

Joako
  • 1,957
  • The law of iterated logarithm $f(t) = \sqrt{2 t \ln \ln t}$ is the correct bound, but only as $t \rightarrow \infty$. What you (and evidently Wikipedia) call the "Modulus of Continuity" is simply the law of iterated logarithm for $t \downarrow 0$. I would guess that $t=500$ is not enough for the LIL bounds to be binding. I suspect your proposed $f$ will be too lose because it effectively involves squaring the $\ln \ln t$ part. – user6247850 Sep 27 '21 at 16:51
  • It is being squared under a square root function where only a constant is added, the same equation could be written as $$f(x)=\sqrt{2t\log{(\log(t+1)+1)}\sqrt{1+\pi^2/\log{(\log(t+1)+1)}^2}}$$ were the "$\pi$"-part will becomes zero when $t \rightarrow \infty$, so I believe that in the limit have the same behaviour as the Law of the Iterated Logarithm – Joako Sep 27 '21 at 17:43
  • Oh, I see, I missed there was an extra square root. Then yes, I agree that these should have the same behavior as $t \rightarrow \infty$. – user6247850 Sep 27 '21 at 17:53
  • @Joako Pictorially, your bounds for LIL seem to be way off. In a sense, the LIL is the optimal result as $t \to \infty$, so it's unclear what you mean by a "better" envelope. Note that to get past the undefined issues, you can define your LIL envelope to be zero when $x < e$. Can you give some clarification as to which type of envelope you are looking for? – Jose Avilez May 18 '22 at 14:35
  • @JoseAvilez Intuitively, I am looking for something like works like a real best "envelope" that will contain "almost-surely" (a.s.) the random paths: LIL will be crossed a.s. infinite many times, and make sense if you see how bad it behaves at the beginning, even when, if I am right, the bounds I proposed are equivalent at $t \to \infty$... I am thinking in something that works like a brownian version of the bound that Lipschitz function have, knowing here are not differentiable, but something that a.s. tells the path are within it, so is not overpass a.s. infinite times. – Joako May 18 '22 at 19:02
  • @JoseAvilez I am not fully sure if the paths I made are 100% well defined as Wiener processes, but if you play with the code you can see that at the beginning the envelope is working pretty good, and in infinite is equivalent to LIL, this is why I believe maybe is a better representation of what the LIL should really wanting to do... and make sense from the point of view of what the modulus of continuity means (if I have understoof it right), how fast can grow the function without becoming discontinuous... but since I made many changes to made it "work", I don't really know if it is just trash – Joako May 18 '22 at 19:08
  • @JoseAvilez By the way, my knowledge related to this is basic.... I self learned from Wikipedia pages, so I don't have enough knowledge to figure out if is fulfilling the probability properties I am aimming to met. – Joako May 18 '22 at 19:10
  • @JoseAvilez But I have seen this kind of envelopes in the past as channels for prices forecast so I think, if this is not mistaken, could have interesting applications. – Joako May 18 '22 at 21:37
  • to myself: since Brownian motion one sigma $\sigma$ bounds are $\sqrt{t}$, at least for a wide range of times the presented bound behave similar to the $\sqrt{\sqrt{2}\pi t}$ curve – Joako Sep 30 '23 at 17:47
  • You do understand that at any moment of time Brownian motion can take any big value with a positive probability, so there won’t be any bounds on its realization, right? – SBF Nov 13 '23 at 15:00
  • @SBF it is why I ask in the probabilistic sense of almost-surely, since conversely, you have also the property that it is a continuous process so in every finite size interval the maximum value must be bounded because of the Extreme Value Theorem... so at least and infinite-size jump is forbidden. – Joako Nov 13 '23 at 17:48
  • There are no finite almost surely (that means probability one) bounds on Brownian motion, which follows from my previous comment, which itself follows from normal distribution of Brownian motion – SBF Nov 14 '23 at 03:11
  • @SBF Could you elaborate? As example the function $f_{\pm}(t)$ I am asking for, if I am not mistaken, fulfills both $$\lim_{t\to 0^+,\ t\to\infty}\sup \dfrac{|w(t)|}{|f_{\pm}(t)|}\overset{\text{a.s.}}{\to} 1$$ so if I am not misunderstanding these formulas shown in wiki for Wiener process in the sections Law of the iterated logarithm and Modulus of continuity, the possible supremum on any interval is increasing as $f_{\pm}(t)$ with probability $1$, so I think I could expect their values being within almost-surely. (...) – Joako Nov 14 '23 at 22:55
  • @SBF (...) Now I am wonder if does something like $b(t)=|f_{\pm}(t)+\epsilon|$ for some $\epsilon >0$ broke somehow this tendency: if the ratio $$\lim_{t\to\infty}\sup \dfrac{|w(t)|}{b(t)}$$ stills goes to a.s. to $1$ for every $\epsilon$ then you are right, but I think it going to make no sense in showing those limits tendencies to begin with (I think Kolmogorov make some of these, so I am expecting they make sense as a prior), (...) – Joako Nov 14 '23 at 22:58
  • @SBF (...) but if conversely, if it broke for some $\epsilon \to 0^+$ then $f_{\pm}(t)$ it is indeed an envelope for the Wiener process: this is what I am trying to figure out (hope it make sense - is quite probably I got things wrong). – Joako Nov 14 '23 at 22:59
  • @SBF The logic I am following is that I have already that $\text{LIL}(t) = \sqrt{2t\log(\log(t))}$ fulfills that $\limsup_{t\to\infty}\dfrac{|w(t)|}{|\text{LIL}(t)|}\overset{\text{a.s.}}{\to} 1$ for a wiener process $w(t)$, and also that $\lim_{t\to\infty}\dfrac{|\text{LIL}(t)|}{|f_{\pm}(t)|}\to 1$, but also that $\lim_{t\to\infty}\dfrac{|\text{LIL}(t)|}{|f_{\pm}(t)+t|}\to 0$ so I believe it must be something in between that works as an envelope. – Joako Nov 15 '23 at 01:05
  • But that’s only about the behavior at infinity – SBF Nov 15 '23 at 04:47
  • @SBF indeed, but it does not imply necessarily it don't work for $t<\infty$, which is what I am asking for. As example in the wiki for Law of the iterated logarithm its presented a plot that kind of show it is fulfilled for all time, and also is mentioned that the Kolmogorov's zero–one law so maybe it is possible to find an envelope that is sharp. I tried to read the papers mentioned in wikipedia but unfortunately I don't understood much about, (...) – Joako Nov 15 '23 at 14:37
  • 1
    Well, definitely there can't be any bounds for $W_t$ with probability $1$ for a fixed $t$ that depend only on $t$ due to the distribution of $W_t$. – SBF Nov 15 '23 at 14:40
  • @SBF (...) Kolmogorov and Khinchin papers are in German, and the others were too advanced for me, so I don´t know how to start to make a prove neither based on those. What I do can tell, is that experimentally I easily made over $+200,000$ realizations of Brownian paths in order to find just one that comes near the edge made by $f_{\pm}(t)$, which is shown in the plot of the question, and also, that for standard unitary 1D random walk, their paths will be surely below the envelope made by the function $f(t)=t$ since at max it could grow on each step by 1 unit. – Joako Nov 15 '23 at 14:41
  • @SBF maybe it could be found the envelope that cannot be over-passed with probability 1: like is within with probability 1, but over the envelope you could show it won't be surpassed infinitely often with probability 1 (as an idea) – Joako Nov 15 '23 at 14:45
  • 1
    Infinitely often is tricky with brwownian motion, it’s “single” crossing may already provide infinite number of points where it crosses another curve – SBF Nov 15 '23 at 14:49

1 Answers1

1

There is no "envelope" that will contain the graph of Brownian motion with probability one for all $t>0$ because of the following support theorem: if $B$ is a standard BM in $\mathbb{R}$ and $f\in C([0,T],\mathbb{R})$ for $T>0$, then for any $\epsilon>0$ $$ \mathbb{P}(\sup_{t\in [0,T]}|B_t-f(t)|<\epsilon)>0. $$

So draw any continuous function $f$ you like, and Brownian motion has a positive probability of being epsilon close to it and thus outside any gauge function you can imagine.

Here are some references

On the other hand by the law of the iterated logarithm we have that almost surely there exists a random $t_{0}$ such that for all $t\geq t_{0}$

$$|B_{t}|\leq 2 \sqrt{2t\log\log t}$$

(eg. Remark 5.2. in Mörters-Peres book on Brownian motion).

So up to any deterministic time $T>0$, BM will not be contained almost-sure in any envelope $\psi(t)$. However, by LIL, there exists a random time $t_{0}(\omega)$ after which BM is contained in the envelope $2 \sqrt{2t\log\log t}$.

Thomas Kojar
  • 7,349
  • Thanks you very much for taking the time to answer. Maybe I am mistaken, but I believe I am asking in principle a slightly different question: what I think the equation you shared said is that there exist always a positive probability for the Brownian motion of achieving any possible envelope function, which is related to their values distributing Normally which have infinite support. But what I aimming to find if there is an envelope that split the path on the region wich values will be matched a.s. infinitely often from others that will not be crossed infinitely often – Joako Nov 15 '23 at 23:01
  • Could you elaborate into this? Maybe the equation you shared already define that every value will be matched a.s. infinitely often but I am not understanding it properly. – Joako Nov 15 '23 at 23:03
  • 1
    @Joako So up to any deterministic time $T>0$, BM will not be contained almost-sure in any envelope $\psi(t)$. However, by LIL, there exists a random time $t_{0}(\omega)$ after which BM is contained in the envelope $2 \sqrt{2t\log\log t}$. This $t_{0}(\omega)$ is not concrete. It changes for each realization. – Thomas Kojar Nov 15 '23 at 23:28
  • Thanks for the book recomendation. I checked the remark $5.2$ and I want to notice the plot shown right before: as the Law of the Iterated Logarithm $\text{LIL}(t)$ makes a tight bound for some big time $t_0$, it fails at shorts times where comes into show the Modulus of Continuity $\text{MOC}(t) = \sqrt{2t\log(\log(1/t))}$ for some $t\to 0^+$, so its kind of too-tight for short times. If you notice the first part of my question the $\text{MOC}(t)$ function becomes complex-valued, so if I take $|\text{MOC}(t)| = \sqrt{2t\sqrt{\pi^2+\log(\log(t))^2}}$ the function I modified for the envelope... – Joako Nov 16 '23 at 00:58
  • so I am trying to figure out if its a better/proper envelope function: at infinity it will fulfill the LIL since $\lim_{t\to\infty} \frac{|\text{LIL}(t)|}{|\text{MOC}(t)|}=1$, but also in principle $|\text{MOC}(t)|>|\text{LIL}(t)|$ for all finite $t$ (caution here since they have problems for small times, so assume I am replacing them with the slightly modified versions I show at the end of the question - but the argument stills stands), this is why I am having the question to beging with (it looks like the natural envelope solution)... – Joako Nov 16 '23 at 01:05
  • I wonder if changing $f_{\pm}(t)$ for the $\text{LIL}(t)$ on the proves shown in chapter $5$ will still find the same results, but unfortunately it is out of the scope of my actual math skills. – Joako Nov 16 '23 at 01:09
  • @Joako As shown above, regardless of what function $\psi(t)$ you pick as the envelope, all you have to do is set $f(t):=\psi(t)+100$ and the BM will be close to it and outside the envelope $\psi(t)$ for $t\leq T$ with positive probability. – Thomas Kojar Nov 16 '23 at 01:09
  • probably I am wrong, but its hard to believe that a continuous process is going to match every possible value a.s. infinitely often in a finite interval $[0,\ T]$, such $0<T<1$ as example, since continuous functions are tide to the Extreme Value Theorem so it must be bounded. Maybe my intuition is wrong (it happen often in probabilities, are not an easy topic for me), but I think it should exist some envelope where the almost surely condition fails to happen to be true. – Joako Nov 16 '23 at 03:22
  • @Joako Extreme value theorem applies here too but separately to each realization of a Brownian motion $|\gamma_{t}(\omega)|\leq B(\omega)$ for $t\in [0,T]$. This $B(\omega)$ can be arbitrarily large with positive probability. – Thomas Kojar Nov 16 '23 at 03:32
  • @Joako If you have any more questions, please feel free to open a new MSE question so that others can help too. – Thomas Kojar Nov 16 '23 at 03:33
  • About your answer I was reviewing the remark 5.2 and its says that the envelope is given by $|B_t|\leq (1+\epsilon)\sqrt{2t\log(\log(t))}$ for some $\epsilon>0$: Why did you choose $(1+\epsilon)=2$? I think that the idea is like assuming $\epsilon \to 0^+$ for defining an envelope, right? – Joako Nov 17 '23 at 00:47
  • 1
    Any epsilon will do. As you take $\epsilon$ smaller, it will actulaly make the upper bound sharper and so the random time larger $t\geq t_{0}(\omega)$. – Thomas Kojar Nov 17 '23 at 03:41