1

enter image description here

Could someone check my solution to the following question?

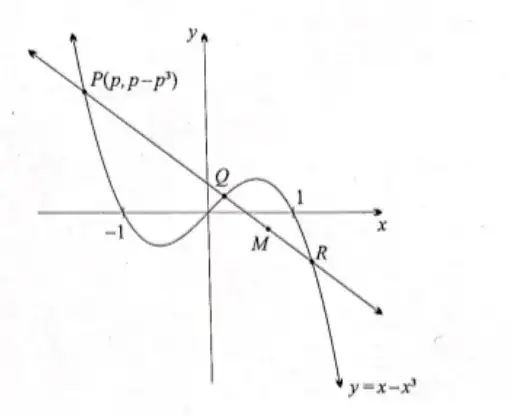
The above image describes the curve $y=x-x^3$ and the line $f(x)=m(x-p)+p-p^3$ where $m$ is the gradient of the line and $p<-1$. The two curves intersect at points $P(p,p-p^3), Q$ and $R$. M is the midpoint of $Q$ and $R$.

i) Find the x-coordinate $M$ and find the gradient of the line that passes through $P$ and is tangent to a distinct point from $P$
ii) Find the range of values for the y-coordinate of $M$ that ensures at least one of the points $Q$ and $R$ is in the first quadrant.

For i) $Q$ and $R$ are the solutions to $x-x^3=m(x-p)+p-p^3$
Which is $x^3+(m-1)x+p(1-m-p^2)=0$
By sum of roots; $x_Q+x_R+p=0$
$\frac{x_Q+x_R}{2}=-\frac{p}{2}$
$\therefore$ the $x$-coordinate of $M$ is $-\frac{p}{2}$
$\frac{dy}{dx}=1-3x^2$
Since the tangent occurs when $Q$ and $R$ converge, it lies on $x=-\frac{p}{2}$
$\therefore m_{tangent}=1-3\left(-\frac{p}{2}\right)^2$
$\therefore m_{tangent}=1-\frac34p^2$

For ii) Range of values for $M$ such that at least one point of $Q$ and/or $R$ is in the first quadrant is between when $f(x)$ is a tangent to a distinct point apart from $P$ as in part i) and when $f(x)$ passes through $Q(0,0)$
To find the minimum, i.e $f(x)$ passes through $Q(0,0)$
$f(x)_{min}=m_{min}x$, substitute $P$
$p-p^3=m_{min}p$
$m_{min}=1-p^2$
$\therefore f(x)_{min}=(1-p^2)x$
Sub $x=-\frac{p}{2}$ to find the $y$-coordinate of $M_{min}$
$y_{min}=(1-p^2)\times\frac{-p}{2}$
$=\frac{p^3}{2}-\frac{p}{2}$

Sub $x=-\frac{p}{2}$ into $y=x-x^3$ to find $y_{max}$
$y_{max}=-\frac{p}{2}-\left(-\frac{p}{2}\right)^3$ $=\frac{p^3}{8}-\frac{p}{2}$
$\therefore \frac{p^3}{2}-\frac{p}{2}<y_M<\frac{p^3}{8}-\frac{p}{2}$

mathlove
  • 151,597
Pen and Paper
  • 1,371

1 Answers1

2

I have not found any errors in your solution, so I think that your solution is correct.

For ii), there is another solution using $m_{tangent}=1-\dfrac34p^2$ though I think that your solution is simpler.

Using Vieta's formulas, one has $$px_Qx_R=-p(1-m-p^2)$$ which implies $$x_Qx_R=m-1+p^2$$ So, the $y$-coordinate of $M$ can be written as $$\begin{align}y_M&=\frac 12(x_Q-x_Q^3+x_R-x_R^3) \\\\&=\frac 12\bigg(x_Q+x_R-(x_Q+x_R)(x_Q^2-x_Qx_R+x_R^2)\bigg) \\\\&=\frac 12\bigg(x_Q+x_R-(x_Q+x_R)((x_Q+x_R)^2-3x_Qx_R)\bigg) \\\\&=\frac 12\bigg(-p-(-p)\bigg((-p)^2-3(m-1+p^2)\bigg)\bigg) \\\\&=\frac{-3p}{2}m-p^3+p\end{align}$$

Since $$1-p^2\lt m\lt 1-\frac 34p^2$$ the range of values for $y_M$ is given by $$\frac{-3p}{2}(1-p^2)-p^3+p\lt y_M\lt \frac{-3p}{2}\bigg(1-\frac 34p^2\bigg)-p^3+p,$$ i.e. $$\frac{p^3}{2}-\frac p2\lt y_M\lt \frac{p^3}{8}-\frac{p}{2}$$

mathlove
  • 151,597