Given a collection $S$ of $N$ segments in the plane, devise an algorithm that decides if there is a line, intersecting all members of $S$ (stabbing line) and, if so, construct it.
Originally this task from Preparata, Shamos "Computational Geometry. An Introducion", exercise 7.2. I don't know where can I begin. There is similar question on math.stackexchange.com, but it doesnot contain an answer.
Maybe you could give some ideas?
Do you now the domain called Integral Geometry that has other names such as Stochastic Geometry, Geometric measure theory ?
In this framework, a straight line, written under its so-called "polar form":
$$x \cos \theta + y \sin \theta = p,$$
is associated with point $(\theta,p)$ in a "cylindrical space" $H$.
Certain sets of lines will be represented as subsets of $H$ with rather remarkable shapes. Dualy, sine curves in $H$ will be associated to points in the ordinary geometrical space.
For example, being given a point $M$ in the ordinary plane with polar coordinates $(\rho_M, \theta_M)$, the set of lines passing through $A$ is represented in $H$ by the sine curve with equation:
$$\rho=\rho_M \cos(\theta-\theta_M)$$
As a consequence, lines that separate 2 points $A$ and $B$, with resp. polar coordinates $(\rho_A, \theta_A)$ and $(\rho_B, \theta_B)$ (which is equivalent to say that such lines intersect segment $[AB]$) are "positionned" in $H$ in the area between the 2 sine curves with equations:
$$\rho=\rho_A \cos(\theta-\theta_A) \ \ \text{and} \ \ \rho=\rho_B \cos(\theta-\theta_B) \tag{1}$$
Therefore, your problem can be implemented in this space by showing that the set of "points" in $H$ (each point representing a line), defined by a set of $n$ constraints of type (1), is non void.
Some references: an answer of mine here. See also there for the result called "Cauchy-Crofton theorem" allowing to attribute a "degree of margin" one can have in such issues using measure theory.
Remark: The transformation I just described is used under the name "Hough Transform" in image processing.
Edit: Here is an apparently different representation using pole polar duality "twining" in a natural way a line to a point, therefore a set of lines to a set of points. In fact this representation is equivalent to the one I have explained before. The big advantage of this representation is that it doesn't need an auxiliary representation space: we always work in the initial space. Technically, it's very simple : to a line with equation $ax+by=1$ is associated its pole $(a,b)$.
Using this correspondence, we can associate to any line segment $[AB]$ the set of lines that intersect it, or more exactly their poles, and the result is simple; the set of lines intersection line segment $[AB]$ is the region situated between the to polar lines of $A$ and $B$ resp. Here is the case (line segment with magenta color). Thousands of random lines intersecting $[AB]$ have been considered and their poles represented by red points materializing the area between the two polar lines of extreme points $A$ and $B$:
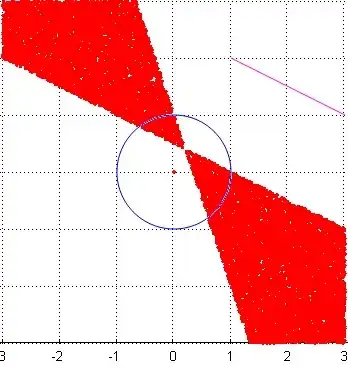
Doing this for line segments $[A_kB_k], \ \ k=1,2...N$ gives a constructive testing method for finding a stabbing line (or proving that none exists) by using simplex method (I must check this idea) which could be a very efficient method.
