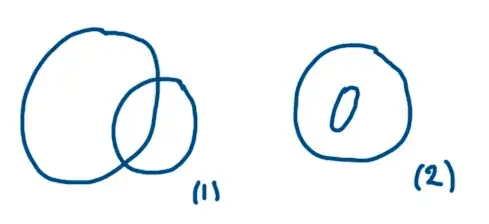I am currently reading an article. It proposes a proof of the Cauchy-Crofton Formula. There are some steps and concepts which I am not completely sure I understand.
(I am also aware of another proof which is slightly different and alas is not of great use for me at the moment.)
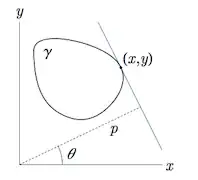
Line on a plane may be defined in the following way:
$$x \cdot \text{cos} \theta + y \cdot \text{sin} \theta - p(\theta) = 0$$ here, $\theta \in [0;2\pi]$ and $p(\theta) \in (-\infty, +\infty)$.
Circumference of closed convex curve(which always has finite length) may be found by the following formula:
$$\text{circumference of } \gamma = \int\limits_{0} ^{2\pi}p(\theta) d\theta$$ where $p(\theta)$ defines tangent to $\gamma$ at a given point. There is nice derivation of this formula in the first paragraph of L. Santalo's "Integral geometry and geometric probability".
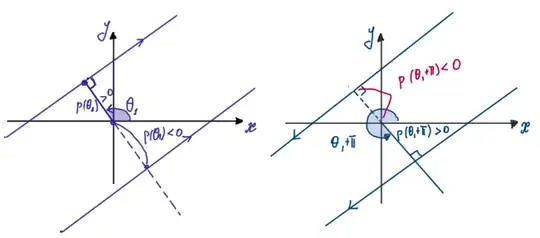
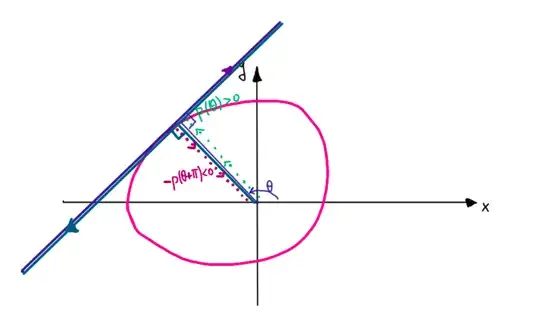
Then authors of the article transform this integral in the following way: $$\text{circumference of } \gamma = \frac{1}{2}\int\limits_{0} ^{2\pi} d\theta \int\limits_{0}^{p(\theta)} dp+ \frac{1}{2}\int\limits_{0} ^{2\pi} d\theta \int\limits^{0}_{-p(\theta)} dp = \frac{1}{2}\int\limits_{0} ^{2\pi} d\theta \int\limits^{p(\theta)}_{-p(\theta+\pi)} dp$$
In order to make sense of integration limits of $p$ I have drawn several pictures. So my first question is whether my intuition about relation of $p(\theta) \text{ and } p(\theta+ \pi)$ is correct?
and also whether I understand correctly what $\int\limits^{p(\theta)}_{-p(\theta+\pi)} dp$ means:
(So I assume that for some fixed $\theta$ for a given curve we have $p(\theta) = p(\theta + \pi)$. Note that $p(\theta)$ defines tangent line to $\gamma$ while $p(\theta + \pi)$ doesn't have to.)
From this point once we shift limits of integration and introduce $n_{\gamma} (\theta, p)$ which counts number of times given line intersect $\gamma$ we essentially obtain Cauchy-Crofton formula:
$$\text{circumference of } \gamma = \frac{1}{4}\int\limits_{0} ^{2\pi} d\theta \int\limits^{+ \infty}_{-\infty} n_{\gamma} (\theta, p) dp$$
Now follows the statement:
The weighting by $n_{\gamma} (\theta, p)$ makes the Crofton formula manifestly additive under concatenation of curves, which allows us to lift the assumptions: $\gamma$ need not be convex or closed
I was not able to find detailed definition of "concatenation of curves". So my second question is whether following two cases are examples of concatenation of curves(and also whether (1) curve is rectifiable)?
Sorry for the length of the question.