Is the golden ratio invariant across non-Euclidean geometries?

Question

I think Pi (the relation between the circumference of a circle and it's diameter) has different values in non-Euclidean geometries. I am interested in what is invariant across all geometries. I wonder if the golden ratio may be invariant across spherical and/or hyperbolic geometries.

Answer 1

Insofar as the Golden Ratio $\phi$ is defined as a number satisfying $\phi^2=\phi+1$ (this is equivalent to the extreme/mean ratio division description), the ratio belongs to any geometry where (loosely speaking) lines are effectively rulers with continuous and uniform real-number labels for points. The existence of $\phi$ in this sense is no more or less remarkable than the existence of $\frac12$. Even $\pi$ as a number exists in such contexts: it lives just past $3$ on the ruler. In a "uniform" geometry (such as the Euclidean, Spherical, and Hyperbolic planes), the rulers don't change from here to there, so the "invariance" of $\phi$ and $\frac12$ and $\pi$ as numbers is baked-in: every segment has a point dividing it in the ratio $1:x$ for any number $x$. As a matter of numerics, there's really nothing to discuss.

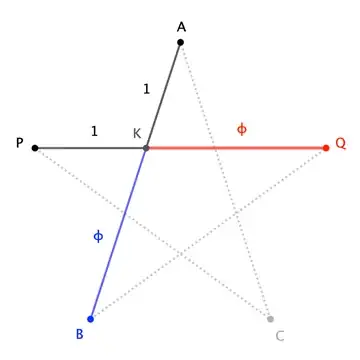
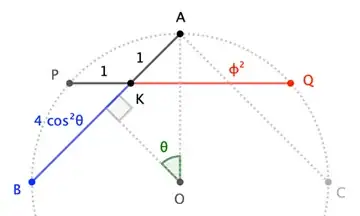
Where things get interesting is investigating whether a value like $\phi$ "arises" from the geometry. For instance, one way $\phi$ arises in Euclidean geometry is via the regular pentagram:

Sides $\overline{AB}$ and $\overline{PQ}$ meet at a point $K$ that divides each of those sides into the ratio $1:\phi$. This construction is "invariant" in Euclidean geometry because all regular pentagrams are similar, and corresponding ratios are preserved by proportionality.

Non-Euclidean geometry lacks similarity: for instance, doubling the lengths sides sharpens the angles of a hyperbolic triangle, and dulls those of a spherical one. So, even if we managed to get a pentagrammic "construction" of the Golden Ratio to work once ...

... we couldn't expect more: larger hyperbolic pentagrams have pointier points (contrariwise for spherical pentagrams), so that the ratio determined by how sides cut each other depends upon scale. Dependence is the antithesis of invariance.

That's not to say, however, that there's nothing to discuss. Indeed, I'm about to launch on a (ahem) lengthy digression ...

---

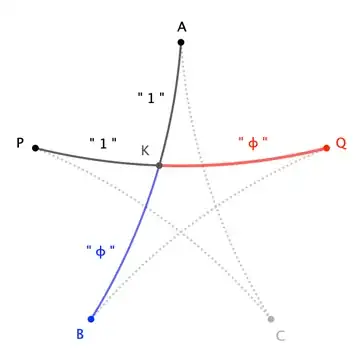
In non-Euclidean geometries "raw lengths", and/or ratios thereof, aren't a primary concern in establishing relations in triangles and other figures. Instead, lengths tend to be wrapped in (circular or hyperbolic) trig functions.

Consider, for instance, the Laws of Sines for a $\triangle ABC$ in Euclidean, Spherical, and Hyperbolic planes: $$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C} \qquad \frac{\sin a}{\sin A}=\frac{\sin b}{\sin B}=\frac{\sin c}{\sin C} \qquad \frac{\sinh a}{\sin A}=\frac{\sinh b}{\sin B}=\frac{\sinh c}{\sin C} \tag1$$ or the circumference of a circle with radius $r$: $$C_{euc} = 2\pi r \qquad C_{sph} = 2\pi \sin r \qquad C_{hyp} = 2\pi \sinh r \tag2$$ While it is true that the circumference-to-"raw"-radius ratio is not invariant, we can establish $\pi$ (and/or $\tau:=2\pi$) as an invariant "circle constant" by defining it in terms of the ratio of circumference and an appropriate transmutation of radius: $$2\pi = \frac{C_{euc}}{r} = \frac{C_{sph}}{\sin r} =\frac{C_{hyp}}{\sinh r} \tag3$$ Likewise for area: $$\pi = \frac{A_{euc}}{4\left(\tfrac12r\right)^2} = \frac{A_{sph}}{4\sin^2\tfrac12r} = \frac{A_{hyp}}{4\sinh^2\tfrac12r}\tag4$$

---

Such transmutation is precisely the mechanism that helps us establish the Golden Ratio as a scale-independent —and thus invariant— "pentagram constant" via the above construction, as we can write:

$$\phi = \frac{|KQ|_{euc}}{|PK|_{euc}} = \frac{\sin |KQ|_{sph}}{\sin |PK|_{sph}} = \frac{\sinh|KQ|_{hyp}}{\sinh|PK|_{hyp}} \tag{5}$$ where $|XY|_{geo}$ indicates distance in the corresponding geometry. (I'll omit the subscript when context is clear.)

Importantly, though, this kind of thing doesn't preserve every kind of ratio. In fact, many (most? all?) of the other occurrences of $\phi$ in the Euclidean pentagram don't transfer to non-Euclidean counterparts simply by swapping every length $\ell$ for $\sin \ell$ or $\sinh \ell$.

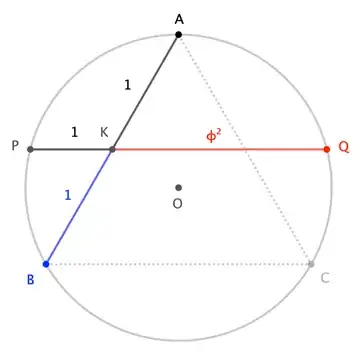
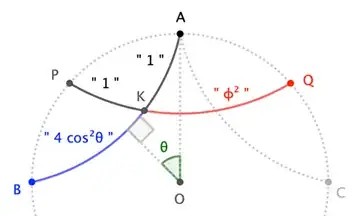
On the other hand, there are other interesting Euclidean occurrences of the Golden Ratio that do have direct non-Euclidean counterparts. For instance, here is a slight restatement of a delightful result from George Odom:

If a midpoint segment of an equilateral triangle is extended to meet the triangle's circumcircle at $P$ and $Q$, then each midpoint divides the extended segment in the square of the Golden Ratio. In particular, for $K$ in the figure, $$\frac{|QK|}{|PK|} = \phi^2 \tag{6}$$

(Odom actually says more-simply that, if $K'$ is the other midpoint, then $$\frac{|KK'|}{|PK|} = \phi \tag{7}$$ a relation equivalent to $(6)$ because $|QK|=|PK|+|KK'|$ and $\phi^2=\phi+1$.)

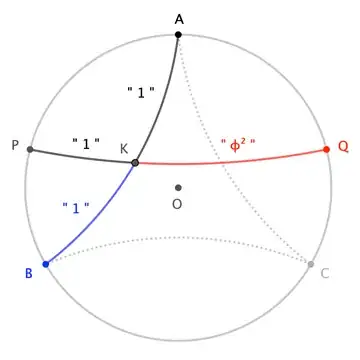
In hyperbolic geometry (spherical is analogous), the same construction "works", provided we apply the "appropriate transmutation" to the lengths:

$$\frac{\sinh|QK|}{\sinh|PK|} = \phi^2 \tag{8}$$

The best we can do for a counterpart to $(7)$ is $$\frac{\sinh|QK|-\sinh|PK|}{\sinh|PK|} = \phi \tag{9}$$ Notice that the numerator does not reduce to $\sinh|KK'|$; as I wrote, the transmutation trick doesn't work for all ratios. (This is why I had to restate Odom's result as a construction of $\phi^2$ instead of $\phi$.)

As a final example where the trick does work (and figures into two aspects of a result), there's this (re-discovered?) generalization of Odom's construction (blog link via trigonography.com):

$$\frac{|BK|}{|AK|} = 4\cos^2\theta \quad\iff\quad \frac{|QK|}{|PK|}=\phi^2 \tag{10}$$ which, eg, in the Hyperbolic plane becomes

$$\frac{\sinh|BK|}{\sinh|AK|} = 4\cos^2\theta \quad\iff\quad \frac{\sinh|QK|}{\sinh|PK|}=\phi^2 \tag{11}$$

---

I'm going to stop typing now. :)

Answer 2

(This is an addendum to Blue's answer.)

In Blue's answer, the constant $\color{blue}{\phi^2}$ figures prominently . We'll see it is also a diagonal of the decagon with unit side length. (Note: All images are from Antonia Buitrago's 2007 article "Polygons, Diagonals, and the Bronze Mean".)

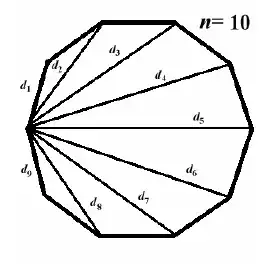
I. Decagon

We follow Buitrago and define a particular set of diagonals $d_k$ as "a line segment joining a common vertex $v_0$ to vertex $v_k$".

Thus $d_1$ is from $v_0$ to $v_1$, while $d_2$ is from $v_0$ to $v_2$, and so on. Of course $d_1 = d_9$ is just the side length of the decagon. The ratio of $d_k$ to $d_1$ is given by,

$$\frac{d_k}{d_1} = \sqrt{\frac{1-\cos\frac{2\pi k}n}{1-\cos\frac{2\pi}n}} = \frac{\sin\frac{\pi k}n}{\sin\frac{\pi}n}$$

Given a decagon with unit side length $d_1 = 1$, choose the third diagonal, then voila,

$$d_3 = \frac{\sin\frac{3\pi}{10}}{\sin\frac{\pi}{10}} = \color{blue}{\phi^2} \approx 2.61803$$

---

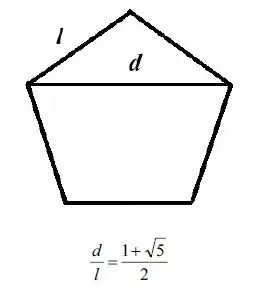
II. Pentagon

For the pentagon with side length $L=d_1=1$, choose the second diagonal,

and we get the well-known appearance of $\phi$ in the pentagon,

$$\frac{d}{L}=\frac{d_2}1 = \frac{\sin\frac{2\pi}{5}}{\sin\frac{\pi}{5}} = \phi \approx 1.61803$$

---

III. The 13-gon

The tridecagon is slightly more complicated, but that's for another post.