5

The artist and amateur mathematician George Odom found this nice construction for the golden ratio $\phi$ using an equilateral triangle and its circumcircle,

$\hskip2.3in$enter image description here $\hskip3.3in$Fig. 1

Let $A$ and $B$ be the midpoints. The ratio of the line segments $|AB|$ and $|BC|$ is, $$R_3 = \frac{|AB|}{|BC|} =\phi$$

We can easily generalize the above figure using a square,

$\hskip2.3in$enter image description here $\hskip3.3in$Fig. 2

Let the (sadly invisible) $A,B,C$ of Fig.2 be analogous to that of Fig.1. What is then its,

$$R_4=\frac{|AB|}{|BC|} =\,?$$

Q: In general, is $R_n$ for $n>3$ algebraic? If it is, does its minimal polynomial have a closed-form?

Tito Piezas III
  • 60,745
  • I haven’t got the time to work this out, unfortunately, but have you tried metallic ratios? – giobrach Feb 06 '18 at 17:32
  • @giobrach: Geometry is not my strong suit, so I will have to wait until someone with expertise comes across this question. – Tito Piezas III Feb 06 '18 at 17:35
  • In the meantime, take a look at this Desmos simulation of the problem for general $n$ that I made: https://www.desmos.com/calculator/flhcoj9nzy – giobrach Feb 06 '18 at 17:56
  • Also, my conjecture is that $R_n \xrightarrow{n\to\infty} 2 + 2\sqrt 2$. – giobrach Feb 06 '18 at 18:02
  • @giobrach: Thanks. It seems for $n=3,4,5,6,7,8$ we have $$-1 - r + r^2 = 0\ - 2 - 2 r + r^2 = 0\1 + 2 r - 2 r^2 - 3 r^3 + r^4 = 0\ - 3 - 3 r + r^2 = 0\ - 1 - 4 r - 3 r^2 + r^3 = 0\2 + 4 r - 2 r^2 - 4 r^3 + r^4 = 0$$ I recognize the case $n=7$, but not the others. Hm. – Tito Piezas III Feb 06 '18 at 18:59
  • I worked on a problem that involved similar polynomials arising from Beraha constants a while ago: https://math.stackexchange.com/questions/2282976/crazy-patterns-arising-from-recursive-sequence-of-functions What I'm guessing is those minimal polynomials are lacking factors that would make them more recognizable. – giobrach Feb 06 '18 at 20:35
  • FYI: Dividing the square's upper edges in the ratio $1:2$ gives Q. H. Tran's Odom-like construction of $\phi$; likewise, dividing the regular hexagon's edges in the ratio $1:3$. (The ratios $1:n$ nicely correspond to the forms $\sqrt{n}/2$ for the sines at "special angles".) See "Special Angles are Golden" (blog link via trigonography.com). See also "Special Angles are Golden, II" for a related construction. See also-also this Math.SE answer for a non-Euclidean take. – Blue Oct 02 '24 at 17:31
  • 1
    @Blue Thanks for the links. I gave an addendum to your MSE answer. It seems $\phi^2$ is not just the square of $\phi$, but is also the length of one of the diagonals of a *decagon* (with side length = $1$). – Tito Piezas III Oct 03 '24 at 04:26

2 Answers2

3

Continuing with giobrach's answer:

We start the simplification by rendering

$\dfrac{1+\cos(\frac{2\pi}{n})}{2}=\cos^2(\frac{\pi}{n})$

So

$R_n=\dfrac{\sin(\frac{2\pi}{n})}{\sqrt{1-\cos^4(\frac{\pi}{n})}-\frac12\sin(\frac{2\pi}{n})}$

We then have

$1-\cos^4(\frac{\pi}{n})=[1+\cos^2(\frac{\pi}{n})][1-\cos^2(\frac{\pi}{n})]=[1+\cos^2(\frac{\pi}{n})]\sin^2(\frac{\pi}{n})$

and

$\sin(\frac{2\pi}{n})=2\sin(\frac{\pi}{n})\cos(\frac{2\pi}{n}),$

from which we can cancel a factor of $\sin(\frac{\pi}{n})$ from the numerator and denominator to get

$R_n=\dfrac{2\cos(\frac{\pi}{n})}{\sqrt{1+\cos^2(\frac{\pi}{n})}-\cos(\frac{\pi}{n})}=[2\cos(\frac{\pi}{n})][\sqrt{1+\cos^2(\frac{\pi}{n})}+\cos(\frac{\pi}{n})]$

This no longer gives the $0/0$ form when $\pi/n\to0$, so a direct substitution leads to

$R_\infty=2+2\sqrt2$

as conjectured.

Both numerical evaluation and Maclaurin series analysis reveal that the truncation term is $O(n^2)$.

Silver and bronze ratios

We generalize the construction in a different way, using nonadjacent sides of some polygons to obtain the silver and bronze ratios.

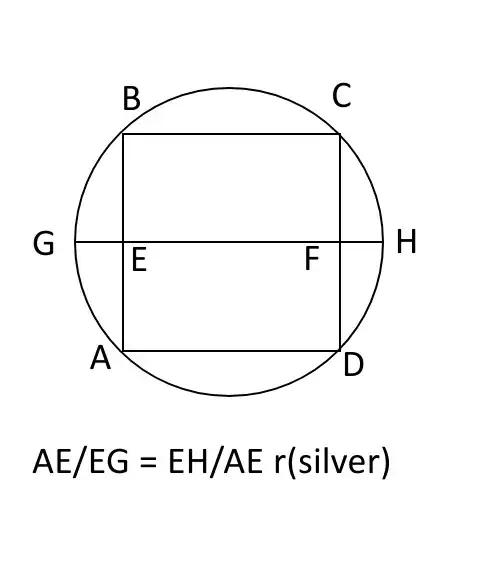
For the silver ratio, begin by inscribing square $ABCD$ in a circle. Construct the chord through the midpoints $E$ of $\overline{AB}$ and $F$ of $\overline{CD}$. This intersects the circle at $G$ nearer to $E$ and $H$ nearer to $F$.

Then the lengths $EG$ and $FH$ are equal, $EF$ is twice $AE$, and $AE$ is the geometric mean between $EG$ and $EH$. These properties guarantee that the ratios $AE/EG$ and $EH/AE$ are both the positive root of $x^2-2x-1=0$, which defines the silver ratio $\sqrt2+1$.

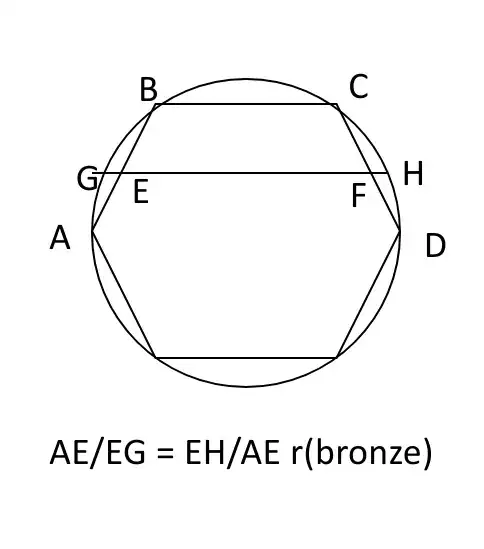
enter image description here

Next, start with a regular hexagon inscribed in a circle. Let $A,B,C,D$ be any four consecutive vertices of the hexagon and then follow the procedure above. This time $EF$ is three times $AE$, so $AE/EG$ and $EH/AE$ satisfy $x^2-3x-1=0$ which defines the brinze ratio $(\sqrt{13}+3)/2$.

enter image description here

Oscar Lanzi
  • 48,208
  • Oh, this is nice. A picture is worth a thousand words. Assuming I’m able, I’ll try to make one someday using the Desmos polygon calculator. – Tito Piezas III Oct 05 '24 at 17:12
2

From purely trigonometric considerations (see this Desmos simulation, or ask if you need clarifications), I've found a closed form for your sequence: $$R_n = \frac{\sin\left(\frac {2\pi}{n}\right)}{\sqrt{1-\left(\frac{1+\cos\left(\frac{2\pi}{n}\right)}{2}\right)^2}-\frac 1 2\sin\left(\frac {2\pi}{n}\right)}$$

It does not look pretty, but I'm sure it can be simplified: I might get back to this when I have more time in my hands. Also have a look at the answers to this question if you want to prove that $R_n$ is algebraic for every $n$.

giobrach
  • 7,852