can graph $K_5$ be embedded in a Möbius band?

Question

I know that $K_5$ can be embedded in torus, but I am not sure if it is possible in Möbius band. Please, can someone explain or show me this?

Thanks.

Answer 1

The answer is yes.

Here a more general question was asked about the criteria for embedding a graph in the Möbius strip. There it was pointed out that graph embedding in a Möbius strip is equivalent to embedding a graph in a projective plane, because cutting out a disk from the latter gives you the former, or equivalently, gluing the former to a disk along their boundaries gives you the latter.

Now since the projective plane can be thought of as a disk with opposite points on the boundary identified, we can actually use the same idea for the torus embedding to construct a projective plane embedding.

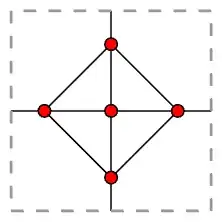
In other words, in the above picture, instead of identifying opposite edges to form a torus, we identify points along the edge that are centrally symmetric to each other. You will notice that the ends of the "broken" edges are still identified to each other, so this picture also illustrates an embedding of $K_5$ into the projective plane.