0

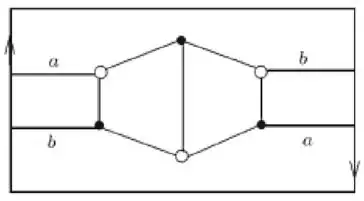
I read the blog below and it says that $K_{3,3}$ can be embedded on the Mobius strip.

In this blog, the author says $K_{3,3}$ can be drawn on the figure as shown:

enter image description here

First encountering such a statement, I believe that it is true.

But when I discussed it with my friends, we realized something might be wrong. Since a Mobius strip is readily available, we created one from paper strips. But I can't draw it in the above way, because edges $a$ and $b$ always cross once. enter image description here

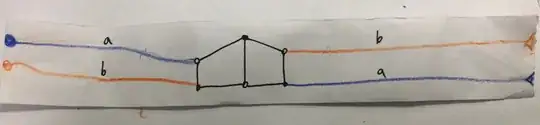
I cut the mobius strip, and no matter what, $a$ and $b$ have to cross once, right. enter image description here enter image description here

Mobius strip seems a little different from the projective plane. We only use the back of the long paper.

I may have misunderstood or misdrawn it. I looked at similar discussions and still found it strange.

licheng
  • 2,687
  • 1
  • 10
  • 25
  • @LeeMosher The author asserts that any edge of $K_{3,3}$ do not cross in his drawing. I follow his method but a and b cross on the Mobius strip. – licheng Jun 19 '22 at 03:39

1 Answers1

3

Your problem is "we only used the back of the long paper". If you use both sides of the long paper you take advantage of the half twist. The twist inverts the arrow in the diagram. You can draw the diagram you show in a small area, then extend the horizontal lines at one end of the diagram around the band twice. You can then identify the two sides of your diagram and are there.

Ross Millikan
  • 383,099
  • I didn't use the right words. I meant we used the back of the paper after the reverse. – licheng Jun 19 '22 at 03:17
  • I made the Mobius strip out by a long strip of paper. So I think I have no problem understanding the concept of Mobius strip. But I didn't draw $K_{3,3}$ so that any edge didn't cross. – licheng Jun 19 '22 at 03:29
  • After you make the Mobius strip there is no front or back to the paper. If you go around once you are on the "other side". If you go around twice you are on the "front side" but upside down. That is exactly what you need to align the two sides of your diagram. The inversion prevents $a$ and $b$ from crossing. Slide the right hand vertical line around the strip once to be on the back side, then again to be on the front and it will be upside down from how it is drawn. You can then identify it with the left vertical. – Ross Millikan Jun 19 '22 at 03:37
  • 2
    The fact that you have drawn marks on the surface of the piece of paper should not deceive you into forgetting that the Möbius band is a 2-dimensional object. When you represent a point of the Möbius band by drawing a dot on the surface of the paper, that point goes "all the way through" the paper; it might be better to think of the paper as being transparent: you can see that point from either side. – Lee Mosher Jun 19 '22 at 03:41
  • 1
    Similarly, when you represent draw an edge of the graph (i.e. the one labelled "$a$") by drawing an arc on the surface of the paper, you should again think of the paper as transparent. The sheet of paper is not an ideal 2-dimensional surface, because it has some very tiny but nonzero thickness, and you are forgetting that the Möbius band being modelled by that piece of paper has no thickness at all. – Lee Mosher Jun 19 '22 at 03:42
  • Thank! I see. As you say, I was deceived by the thickness and opacity of the paper. – licheng Jun 19 '22 at 04:39