About Fano plane symmetries

Question

I have been looking for realizations of order $21$ metacyclic group. I asked about this yesterday and learned some very good information about it Realization of the metacyclic group of order 21

I was also experimenting with the Fano plane and accidentally discovered something I can't explain. I numbered the binary codes and considered the permutations that cycle through them in order, and the permutations that rotate the bits:

001, 010, 011, 100, 101, 110, and 111
1    2     3    4     5   6       7
gap> StructureDescription(Group((1,2,3,4,5,6,7), (1,2,4)(3,6,5)));
"C7 : C3"

This is the metacyclic group. But I then looked at the Fano plane and saw that the cycle should be $(7,6,4,3,5,1,2)$. This cycle produces $\text{PSL}(3,2)$. I also found that the cycle $(7,6,4,3,5,1,2)$ produces $A7$. So I was very confused because the first thing I tried produced the group I was interested in, but when I look now at the Fano plane this $7$-cycle seems meaningless/random.

What is the geometric meaning of this $7$-cycle permutation in terms of the fano plane?

Answer 1

What is the geometric meaning of this 7-cycle permutation in terms of the fano plane?

The Fano Plane is the projective plane $\mathbb{P}(\mathbb{F}_2^3)$. The 1D subspaces of $\mathbb{F}_2^3$ (so, nonzero vectors, because $\mathbb{F}_2$) are represented by "points," and the 2D subspaces of $\mathbb{F}_2^3$, each containing three 1D subspaces, are projective "lines." Clearly $\mathbb{F}_2^3$ and hence the Fano plane has $3$-fold symmetry; the following typical illustration makes the $S_3$ symmetry evident:

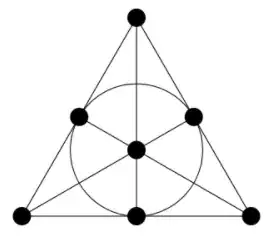
There are some aspects of the Fano plane this picture obscures, however. In particular, while projective lines are understood to be $3$-cycles in this graph above, most of these $3$-cycles have a hidden edge! All of the straight lines are understood to "wrap around" in order to be interpreted as circles of sorts. As a result, the central node is distinguished from all the rest, and this breaks the symmetry of the actual Fano plane, in which all points and all lines are indistinguishable (i.e. the symmetry group acts transitively on them).

The symmetry group $G$ of the Fano plane has size

$$ |\mathrm{PGL}_3(\mathbb{F}_2)|=(2^3-1)(2^3-2)(2^3-2^2)=7\cdot24=168. $$

---

Aside: This also indicates there ought to be some kind of $4$- or $8$-fold symmetry to the Fano plane that should somehow be depictable. Indeed, if we take the outside edge midpoints of the above depiction, and pull them out a bit, we can see a hexagon, and from there if we pull them out of the page (or screen) we get a triangular antiprism, i.e. an octahedron, but with a center point connected via edges to the other six vertices.

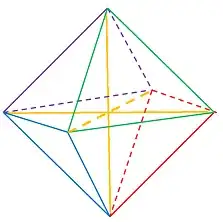
These "axes" through the center are understood to "wrap around" just as the internal lines of the earlier depiction did. Moreover, if we checkerboard the faces (i.e. paint with two colors so adjacent faces are different colors), the corresponding triangles of first-colored faces are also projective lines. The symmetry group of this checkerboard octahedron, and hence a symmetry subgroup of the Fano plane's, is $S_4$. In some sense, this does "better" than the usual Fano plane depiction because it clearly includes the earlier $S_3$ symmetry subgroup (as rotations around a face plus some reflections; it stabilizes an opposite pair of faces).

To see this, first consider the full symmetry group of an octahedron. The rotational symmetry group is $S_4$, same as the cube (great exercise), plus the central improper reflection $-I_3$ brings the octahedral symmetry group to be $S_4\times\mathbb{Z}_2$. By inspection, only the even permutations (of the four space diagonals through antipodal face midpoints) are possible with checkerboard-preserving rotations, and only proper plane reflections preserve the checkerboard patter, hence the symmetry group is $(A_4\times\{I_3\})\sqcup(S_4\setminus A_4\times\{-I_3\})$ which is an isomorphic copy of $S_4$ (which has been "twisted" from the obvious copy in $S_4\times\mathbb{Z}_2$).

In fact, this $S_4$ is the stabilizer of $111$, the central node, because it is index $7$, or see

$$ \mathrm{Stab}(111)\cong\mathrm{Aff}_2(\mathbb{F}_2)\cong\mathbb{F}_2^2\rtimes\mathrm{GL}_2(\mathbb{F}_2)\cong V_4\rtimes S_3 \cong S_4. $$

Above, we use: (a) the usual way of putting an affine group in a general linear group of one higher dimension (as block matrices with last row or column a standard basis coordinate vector), (b) the exceptional isomorphism $\mathrm{GL}_2(\mathbb{F}_2)=S_3$, and (c) the exceptional (among symmetric groups) fact that $S_4$ is a semidirect product.

---

By Cauchy's theorem, $G$ must have an element of order $7$, which must be a $7$-cycle (since it acts nontrivially on a set of size $7$), so the Fano plane also must have $7$-fold symmetry somehow.

To see how (visually), we will make use of the exceptional isomorphism

$$ \mathrm{PGL}_3(\mathbb{F}_2)\cong \mathrm{PSL}_2(\mathbb{F}_7). $$

There are many arguments that show this, some are elementary, but none I find satisfyingly "natural" and "a priori," unfortunately. At any rate, we can check its size matches:

$$ |\mathrm{PSL}_2(\mathbb{F}_7)|=\frac{(7^2-1)(7^2-7)}{2(7-1)}=168. $$

We will reconstruct the Fano plane, with $7$-fold symmetry, by observing how it can be constructed from $\mathrm{PGL}_3(\mathbb{F}_2)$ and transporting details over to $\mathrm{PSL}_2(\mathbb{F}_7)$.

---

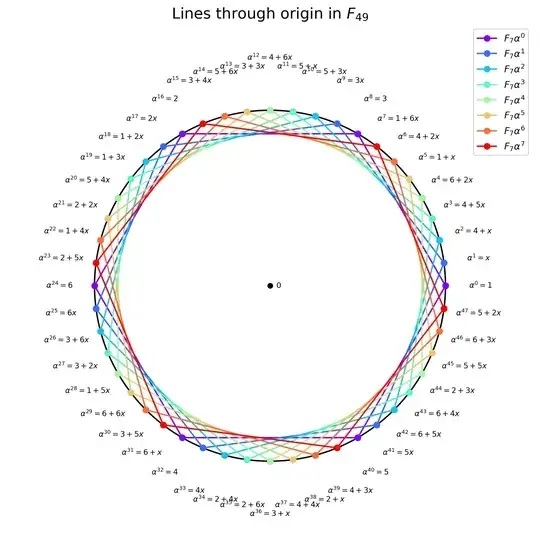
Notice cycling the coordinates of $\mathbb{F}_2^3$ has cycle type $(\cdot\cdot\cdot)(\cdot\cdot\cdot)$ on the Fano plane (fixing $111$, with orbits $100,010,001$ and $110,101,011$). (Or, equivalently, $\mathrm{PGL}_2(\mathbb{F}_2)=S_3$'s $3$-cycle acting on the Fano plane has two orbits corresponding to the last coordinate being $0$ or $1$. In this case, the fixed point is $001$ instead of $111$.) One of these has an orbit which is a projective line, as rotating the typical illustration of the Fano plane is a projective symmetry and the (actual) circle in it is a projective line. (This projective line is comprised of the cyclings of $110$.) All $3$-cycles are conjugate in $\mathrm{PGL}_3(\mathbb{F}_2)$ (by Sylow theory) so this applies to all of them. If we apply a nontrivial $7$-cycle to a projective line, we must get all $7$ projective lines.

Thus, we may construct the Fano plane simply using this metacyclic group $\mathbb{Z}_7\rtimes\mathbb{Z}_3$'s action on $\mathbb{Z}_7$ (note $\mathbb{Z}_7\rtimes\mathbb{Z}_3$ is a subgroup of the holomorph $\mathrm{Hol}(\mathbb{Z}_7)$, which is the "affine group" $\mathrm{Aff}_1(\mathbb{F}_7)$, so $\mathbb{Z}_7$ acts on itself regularly and $\mathbb{Z}_3$ acts on $\mathbb{Z}_7$ by group automorphisms). This can be done within $\mathrm{PSL}_2(\mathbb{F}_7)$ to come up with a labelling scheme.

The group $\mathrm{PSL}_2(\mathbb{F}_7)$ acting on the projective line $\mathbb{F}_7\mathbb{P}^1=\mathbb{F}_7\cup\{\infty\}$ by Mobius transformations has stabilizer subgroup $\mathrm{Stab}(\infty)=\mathbb{Z}_7\rtimes\mathbb{Z}_3$ acting by affine functions of $\mathbb{F}_7$ of the form $f(x)=a^2x+b$ ($a\ne0$) corresponding to matrices $\pm[\begin{smallmatrix} a & b \\ 0 & a^{-1}\end{smallmatrix}]$ in $\mathrm{PSL}_2(\mathbb{F}_7)$, which is kind of like being $\mathrm{Aff}_1(\mathbb{F}_7)\cong\mathbb{Z}_7\rtimes\mathbb{Z}_6$ but not quite (also note $G$ has no order $6$ element).

Because $2^3\equiv1$ mod $7$, the map $x\mapsto 2x$ has order $3$. One of its nontrivial orbits is $\{1,2,4\}$, which we will declare to be a projective line. There should be $7$ projective lines, and the symmetry group should act on them transitively, so we should get all new projective lines in our new model by translating $\{1,2,4\}$. It suffices to translate the projective line using the $7$-cycle $x\mapsto x+1$, an affine function. Thus, our points are $\{1,2,\cdots,7\}$ and our lines are $\{a+1,a+2,a+4\}$.

[Since Mobius transformations (which is how $\mathrm{PSL}_2(\mathbb{F}_7)$ acts on $\mathbb{F}_7\cup\{\infty\}$, whose elements represent points of the projective line $\mathbb{P}(\mathbb{F}_7^2)$) preserve cross-ratio, we can observe these projective lines (in our new Fano plane model) are those triples with a specified cross-ratio. Just an aside.]

This gives us the following picture of the Fano plane:

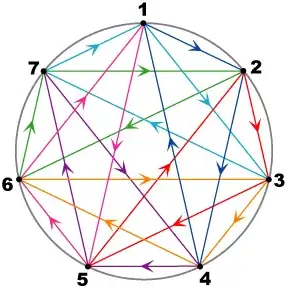
Each colored triangle is a projective line. This is the complete graph $K_7$, so there are no "missing" or "hidden" edges in this model, unlike the other model. (The triangles are oriented to describe an octonion multiplication table.)

We can remove exactly one edge from each triangle to get another picture, with "hidden edges" in the projective lines, just like the original picture, but which nonetheless illustrates the $7$-fold symmetry and has no distinguished points or lines:

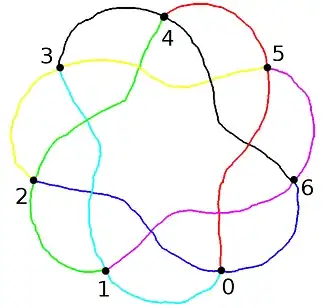
Some thoughts. (a) This construction only used the metacyclic subgroup $\mathrm{Stab}(\infty)=\mathbb{Z}_7\rtimes\mathbb{Z}_3$ of $\mathrm{PSL}_2(\mathbb{F}_7)$, not the whole thing. So, (b) it certainly doesn't illustrate why $\mathrm{PGL}_3(\mathbb{F}_2)=\mathrm{PSL}_2(\mathbb{F}_7)$, and indeed (c) the action of $\mathrm{PSL}_2(\mathbb{F}_7)$ of on $\mathbb{F}_7$ is unclear to me - in particular, it is no longer by Mobius transformations, since they're transitive on the $8$-element set $\mathbb{F}_7\cup\{\infty\}$.

The fact that $\mathrm{PSL}_2(\mathbb{F}_7)$ acts transitively on sets of both sizes $7$ and $8$ is strikingly identical to the fact $\mathrm{Spin}(7)$ acts irreducibly on both $\mathbb{R}^7$ (via rotations) and $\mathbb{R}^8$ (via octonions). Perhaps there's a deeper connection to be found by answering "what is the $\mathbb{F}_1$ version of octonions?"

Answer 2

The projective line over $F_7$ can be viewed as lines through the origin in $F_{49}$. Here $F_{49} \cong F_7[x]/(x^2+6x+3) \cong F_7(\alpha)$, so $\{1,x\}$ is a basis and $\alpha \equiv x$.

$PF_7 \cong \left(F_{49}\setminus\{0\}\right)/(\lambda f \sim f)$. We obtain eight lines in total, and can mark them by their "inital" points $\{\alpha^0=1, \alpha^1, \ldots, \alpha^7\}$. These correspond to classes $[k:1]$ for $k \in F_7$ along with $[1:0]$, the point at infinity. $k$ is the "slope" since $[x:y]=[x/y:1]$ for $y \ne 0$, and we can view $PF_7 \cong \{\infty\} \cup F_7$.

Then we can look at the two dim'l representations of symmetries as matrices, and their corresponding linear fractional transformations.

The three generators are inversion (order 2), doubling (order 3), and rotation (order 7).

Reflection: $r: k \mapsto -1/k$, $\begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}$, $[x:y] \mapsto [-y:x]$. $\infty \mapsto 0$, $0 \mapsto \infty$, $1 \mapsto -1$. This swaps $[1:0]$ with $[0:1]$.

Translation: $t: k \mapsto k+1$, $\begin{pmatrix} 1 & 1 \\ 0 & 1 \end{pmatrix}$, $[x:y] \mapsto [x+y:y] = [x/y+1:1]$. $\infty \mapsto \infty$, $0 \mapsto 1$, $1 \mapsto 2$. $[1:0]$ is fixed. For $y \ne 0$, $[x+y:y] = [x/y+1:1]$, so $[k:1] \mapsto [k+1:1]$. This shear map rotates each line by one place counterclockwise.

Doubling: $\delta: k \mapsto 2k$, $\begin{pmatrix} 2 & 0 \\ 0 & 1 \end{pmatrix}$, $[k:1] \mapsto [2k:1]$. $\infty \mapsto \infty$, $0 \mapsto 0$, $1 \mapsto 2$. Since $2^3 \equiv 8 \, (\text{mod } 7)$, this is order 3.

Now we connect these symmetries to that of the Fano plane.

Let $F_8 = F_2[x]/(x^3+x+1)$, so $F_8^{\times} = \langle x \rangle$. Then $F_8 = \{x^{\infty}=0,x^{0}=1,x^1, \ldots, x^6\} = \{x^k : k \in PF_7\}$.

$F_8 \cong F_2^3$ as vector spaces, so can be used to construct the projective plane $P^2F_2 = F_8 \setminus 0 = F_8^{\times}$.

Define a function on special linear fractional transformations which will turn out to be an isomorphism:

$$T: SLF(7) \rightarrow GL(F_8)$$ $$T_f: x \mapsto x^{f(k)} + x^{f(\infty)}$$

where we include the second term for linearity. Note that $B=\{1,x,x^2\}$ is a basis for $F_8$ since $x^3 = x+1$.

$[T_r]_B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$. This swaps the two basis vectors $\{x,x^2\}$.

$[T_t]_B = \begin{pmatrix} 0 & 0 & 1 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{pmatrix}$. For $k \ne \infty$, $T_t(x^k) = x^{t(k)}+x^{t(\infty)} = x^{k+1} = x(x^k)$, so $T_t$ acts as multiplication by $x$ in $F_8$.

$[T_\delta]_B = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix}$. For $k \ne \infty$, $T_\delta(x^k) = x^{\delta(k)} = x^{2k} = (x^k)^2$ is the squaring map.

To answer the question re: the order 7 symmetry, there happens to be an isomorphism of the symmetries of $PF_7$ and $F_8$ (and an identification of point sets, but not their algebraic structure), and in this identification the "add 1 to slope" translation symmetry in $PF_7$ corresponds to "multiply by multiplicative generator" in $F_8$.

n.b. I am summarizing the exposition in Why is PSL(2, 7)∼ = GL(3, 2)?.