3

if the equation of the curve of the reflection of ellipse $ \frac{(x-4)^2}{16} + \frac{ (y-3)^2}{9} = 1$ about the line $x-y-2=0$ is $16x^2 + 9y^2 + k_1 x -36 y+k_2 =0 $ , then $ \frac{k_1 +k_2}{33}$ =?

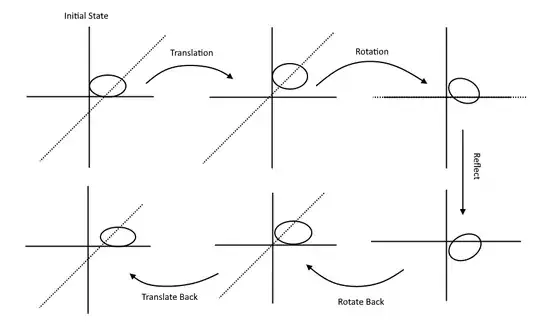
So, I thought of this method using complex numbers to find reflection point (z'), so say I want to reflect a point $ z=(x+iy)$ about a line, then I do this sequence of transformation.

$$ z' = \overline{z} e^{ 2i \arctan(m) } $$

where 'm' is slope of line,

So, I first do a coordinate transform for the ellipse

$ x= 4 + 4 \cos \theta$

$ y = 3 + 3 \sin \theta$

And thne,

I put $ z= (4 + 4 \cos \theta) + i( 3+ 3 \sin \theta)$

$\overline{z} = (4 +4 \cos \theta) - i (3 + 3 \sin \theta)$

so, $ m= \frac{\pi}{4}$

I get,

$ z' = \overline{z} (i)$\

but this doesn't give me the right answer for some reason...

P.s: the motivation for the reflection point formula is that, first I make the line my x axis byrotating whole plane by negative of slope of line i.e : \overline{ z e^{i \arctan(m)} , then to find reflection I took reflection of this point about 'x' axis by conjugating it then I multiply it by $ e^{ i \arctan(m)} $ to find the point in original coordinate system

Where exactly am I going wrong?

If the equation of the curve on the reflection of the ellipse $\frac{(x-4)^2}{16}+\frac{(y-3)^2}{9}=1$ about the line $x-y-2=0$ is ...

I saw this, but I want to do this using complex numbers reference for my method:

enter image description here

  1. I make my line of refleciton my axis
  2. I conjugate my point
  3. I rotate my point back by how much I rotated it originally

Part that I am confused with : Why do we shift the line such that intercepts line up with origin? I know we either shift x intercept to origin or y intercept to origin coz x intercept and y intercept related. But why do we start with this?

Clemens Bartholdy
  • 14,222

3 Answers3

1

The diagram is on the right track, but you will also have to do a translation given the fact that $y=x-2$.

The steps as I would envision are:

  1. Make the following substitutions: $$ x = \frac{z+ \overline{z}}{2}$$ $$ y = \frac{z- \overline{z}}{2i}$$

  2. Apply the rotational coordinate transformation: $$ z' = ze^{-i\theta}$$ $$\theta = artcan(m)$$

  3. Apply the translation coordinate transformation: $$ z'' = z' + ai $$ $$ a = \sqrt{2} $$

  4. Perform the reflection: $$ z'' = \overline{z''}$$

  5. 'Undo' the translation coordinate transformation: $$ z' = z'' - ai $$

  6. 'Undo' the rotational coordinate transformation: $$ z = z'e^{i\theta}$$

Diagram of translation first approach (Ellipse position is very approximate): enter image description here

gigo318
  • 503
  • The translation step is what is throwing me of... can you explain that one further in more detail? – Clemens Bartholdy Jul 13 '20 at 19:19
  • Since the complex conjugate mirrors values over the x-axis, you need to translate the complex plane such that the line y=-2 overlaps the origin. For instance if you want to reflect the point z = 0 + 4i about the line "y = -2", then you need to 1) shift the plane up two units giving z' = 0 + 6i 2) perform the complex conjugation giving z' = 0 - 6i 3) undo the shift up giving z = 0 - 8i. – gigo318 Jul 13 '20 at 19:28
  • FYI, I made an error in the upwards translation needed. The up shift should be sqrt(2) instead of 2 as I originally put. This is because after the line y=x-2 is rotated clockwise by 45 deg. the line will become y=-sqrt(2) and NOT y=-2. Note that $\abs{a}$ is simply the shortest distance from the origin to the line y=x-2. – gigo318 Jul 13 '20 at 20:09
  • why specifically do we want y intercept to overlap origin? can't we make x intercept over lap w/ origin – Clemens Bartholdy Jul 13 '20 at 20:14
  • Well we don't just want the y-intercept to overlap the origin. We want the entire line to overlap the x-axis. After the first rotation, the line will have zero slope (i.e. of the form y = b). Since the line will be parallel to the x-axis after the rotation, a translation will move the line to to origin. – gigo318 Jul 13 '20 at 20:24
  • I just realized that x intercept and y intercept are related, so as we change x intercept, we chagne y intercept – Clemens Bartholdy Jul 14 '20 at 16:54
  • so, we just need to make it either that X intercept over laps with origin or the Y – Clemens Bartholdy Jul 14 '20 at 16:58
  • I think I understand more clearly what your questions is. The reason to move the Y-intercept to origin (as originally asked) is to make is so that a subsequent rotation of the plane will cause the line of reflection to overlap the x-axis. This works if you first translate the plane, and then rotate the plane. In my answer, I first rotated the plane and then translated it to get the line of reflection to overlap the origin. In both cases, in order to use the complex conjugate to perform the reflection you must have the line of reflection be the x axis; hence all the translations and rotations – gigo318 Jul 14 '20 at 17:18
  • could you supplement your answer with a pic? I think it is the best but needs a few more pictures – Clemens Bartholdy Jul 14 '20 at 17:19
  • Just added one, hope it helps clarify. – gigo318 Jul 14 '20 at 19:27
  • the diagram feels like I'd get different results if I shifted to y intercept or x intercept, what would happend if I rotated before shifting? – Clemens Bartholdy Jul 14 '20 at 19:39
  • What do you think would happen? – gigo318 Jul 14 '20 at 19:52
  • I think it would still overlap with x axis – Clemens Bartholdy Jul 14 '20 at 20:14
  • I think this will explain what happens if you rotate without any translations: https://www.desmos.com/calculator/vyqnhtoty7 – gigo318 Jul 14 '20 at 22:49
  • at t=-5.5 it overlaps sitll – Clemens Bartholdy Jul 14 '20 at 23:01
  • It overlaps the line $y=-\sqrt{2}$ not the x-axis – gigo318 Jul 15 '20 at 00:30
0

I've got a result which is analogous to reflection of a point w.r.t. a line in Cartesian coordinates.

After following the step 1 in the answer of @gigo318, you get the complex equation of the line as $$a\overline z+\overline az+b=0$$ Now, the reflection of the point $z_1$ about this line can be given as

$$\begin{align*}\displaystyle\frac{(z+\overline z) -(z_1+\overline{z_1})}{a+\overline a}=\frac{(z-\overline z)-(z_1-\overline{z_1})}{a-\overline a}&=\frac{-(a\overline{z_1}+\overline az_1+b)}{|a|^2}\end{align*}$$

SarGe
  • 3,061
0

Conceptually, what you are doing in the complex plane is to rotate the line of reflection to the horizontal, take the conjugate, and rotate it back by the same angle. So, say you have a line from $z_1$ to $z_2$, at an angle $\alpha=\tan^{-1}(m)$ and you want the reflection of point $z$, say $z'$.

Then

$$ \begin{align*} z'=\big((z-z_1)e^{-i\alpha}\big)^*e^{i\alpha}+z_1\ &=(z^*-z_1^*)e^{i2\alpha}+z_1 \end{align*}$$

Cye Waldman
  • 8,196
  • what is z'? and why did you add $ z_1$ – Clemens Bartholdy Jul 14 '20 at 16:58
  • I thought that $z'$ was what you are using for the reflection. You subtract $z_1$ so the the rotation takes at the origin, otherwise, you would be rotating the entire field. Then you add back $z_1$ to put it in the right place. This is the sort of thing that complex variables can do very simply compared with Cartesian coordinates. – Cye Waldman Jul 14 '20 at 23:24