3

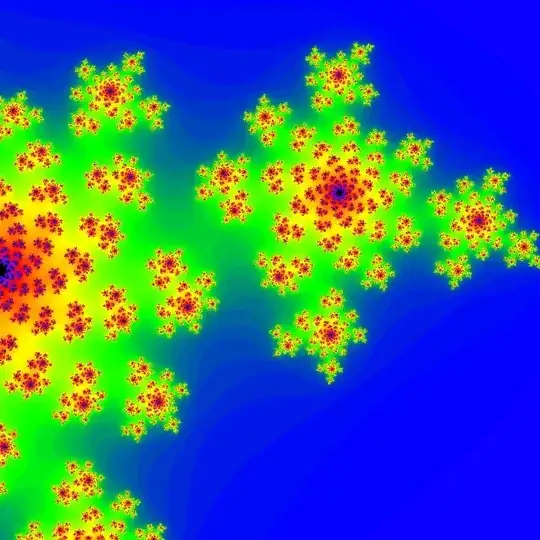
After reading through this question about Misiurewicz Points in the Mandelbrot set, I got curious on how to compute the critical points for Julia sets. At the core, what I want to determine is a fast algorithm that, given c, create a sequential list of n critical points (I really only care about the first two points, but finding n points would be nice to know). For instance, in the image below, the first 2 points would be the two center points where the largest number of "islands" surround.

Unfortunately, I haven't found many resources on this topic, and I spent a lot of time looking. Perhaps I don't know the right terms to use, or what I'm looking for doesn't exist, and my own efforts to figure it out have not worked. I read through here as well, but I'm not sure how I can use that knowledge to help me with my problem.

Any pointers in the right direction would be amazing!

enter image description here

Edit:

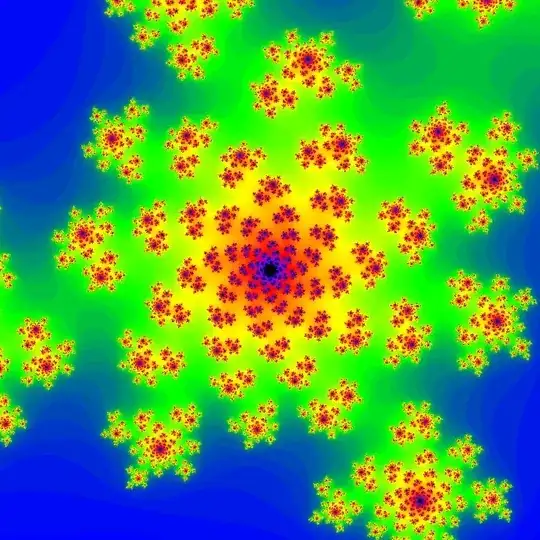
Thanks to Claude in the comments, I know the what terms to use now and figured out the correct formula to use (for the first critical points): $\frac{1 - \sqrt{1 - 4c}}{2}$

At first, I discovered this paper, which states in Definition 2.2 that "The attractor basin of infinity is never all of C since $f_c$ has fixed points $z_f=1/2\pm\sqrt{1/4 + c}$", but this gave the wrong point I was looking for, as seen in the first image below. But then I discovered a different question with the formula for fixed points that I was looking for, which ended up just being one of the algebraic solutions to $z_{p+1}=z_p^2+c$ where $p$ is $0$ (shown in the last image below).

enter image description here

enter image description here

Ibrahim Mahmoud
  • 469
  • I think you want fixed points and pre-images of fixed points, rather than critical points. A fixed point $z_0$ will satisfy $z_0 = z_0^2 + c$, while a pre-image of a fixed point will satisfy $z_p = z_p^2 + c$ after $p$ iterations (starting from $z_0$). – Claude Jun 23 '20 at 02:44

0 Answers0