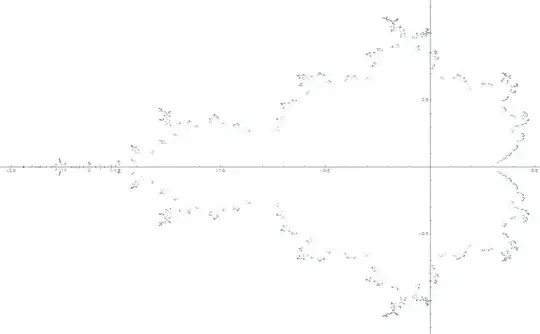
Here is a plot of 17,723 Misiurewicz Points. The code below generates a set of polynomials u[m,n], the roots of which have periodicity (m-n) starting at iteration n. I stopped at 17,723 points because to get more by this method I had to generate and solve $2^{11}$-order polynomials. In other words, I hit the practical limit of my method.
So my question is: Is there any way I can find more Misiurewicz points without having to solve giant polynomials?
This relates to another Question about the right-most real Misiurewicz Point.
Mathematica code:
z[n_, c_] := If[n > 0, z[n - 1, c]^2 + c, c];
ord = 8;
(* Calculate u[m,n] up to m==ord *)
Do[Do[
If[n > 0, t = Expand[z[m, c] - z[n, c]], t = Expand[z[m - 1, c]]];
p = m - n;
Do[Do[If[((i != m) || (j != n)) && (Mod[p, i - j] == 0),
While[(tt = PolynomialQuotientRemainder[t, u[i, j], c])[[2]] == 0, t = tt[[1]]]], {j, 0, Min[n, i - 1]}], {i, 1, m}];
u[m, n] = t, {n, 0, m - 1}], {m, 1, ord}];
Print["Polynomial orders : ", Table[Exponent[u[m, n], c], {m, 1, ord}, {n, 0, m - 1}] // MatrixForm];
(* Compile numerical roots of u[m,n>0], which are c's on the edge of the M-set *)
plotOrd = 8;
$MaxRootDegree = Max[$MaxRootDegree, 2^(plotOrd - 1)];
rts = {};
Do[
Do[
s[m, n] = Solve[u[m, n] == 0, c] // N;
rts = Append[rts, c /. s[m, n]], {n, 1, m - 1}], {m, 1, plotOrd}];
rts = Flatten[rts];
Print["Number of Plot points : ", Length[rts]];
Print[ListPlot[Transpose[{Re[rts], Im[rts]}],PlotStyle ->PointSize[Small]]];
These settings will produce a plot in few seconds. The jpeg above took a while and was generated with
ord=11;
plotOrd=11;
and
Print[ListPlot[Transpose[{Re[rts], Im[rts]}],PlotStyle ->PointSize[Tiny]]];