On each side of a quadrilateral $ABCD$, squares are drawn. The centers of the opposite squares are joined. Show that $PR$ and $QS$ are perpendicular to each other and equal in magnitude.
Pure geometry is becoming very lengthy, perhaps difficult. Also, since, quadrilateral is arbitrary use of coordinate geometry is not proving much helpful.
Let the lower case letter represent the point in the complex plane. (e.g $a$ represents $A$).
Then $p=a+z(b-a),q=b+z(c-b),r=c+z(d-c),s=d+z(a-d)$ for $z=\frac{i+1}{2}$
Thus $$p-r=a-c+z(b-d-a+c)=\bar{z}(a-c)+z(b-d)$$ and $$q-s=b-d+z(c-a-b+d)=\bar{z}(b-d)+(a-c)$$.
But since $z=i\bar z$ they are equal and perpendicular.
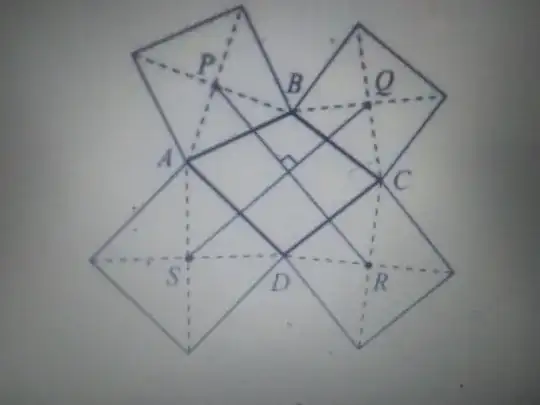
To rotate vector around any point by some angle it says to rotate this vector by this angle around a tail of the vector.
Let $R^{\alpha}(\vec{a})$ be a rotation of $\vec{a}$ by $\alpha$ and $AA_1B_2B$, $BB_1C_2C$, $CC_1D_2D$ and $DD_1A_2A$ be our squares.
Thus, we need to prove that $$R^{90^{\circ}}(\vec{SQ})=\vec{RP}.$$ Indeed, $$R^{90^{\circ}}(\vec{SQ})=R^{90^{\circ}}\left(\vec{SD}+\vec{DR}+\vec{RC}+\vec{CQ}\right)=\vec{SA}+\vec{RC}+\vec{RD}+\vec{QB}$$ and it's enough to prove that: $$\vec{RC}+\vec{CQ}+\vec{QB}+\vec{BP}=\vec{SA}+\vec{RC}+\vec{RD}+\vec{QB}$$ or $$\vec{CQ}+\vec{BP}=\vec{SA}+\vec{RD}$$ or $$\vec{DR}+\vec{CQ}+\vec{BP}+\vec{AS}=\vec{0},$$ which is true because $$\sqrt2R^{45^{\circ}}\left(\vec{DR}+\vec{CQ}+\vec{BP}+\vec{AS}\right)=\vec{DC}+\vec{CB}+\vec{BA}+\vec{AD}=\vec{0}.$$
