Are these theorems about squares known?

Question

Yesterday, while playing with the GeoGebra app, I discovered some properties of squares. I am not sure whether they are already known or not.

---

First Observation:

In the given figure, we construct squares on the sides of an arbitrary quadrilateral in the same orientation. The green points represent the midpoints of the dotted lines. Then, the following properties hold:

1. The two green lines are perpendicular.

2. The two green lines are equal in length.

Additional properties related to Van Aubel's Theorem:

3. The length of the line formed in this theorem equals the length of the line formed in Van Aubel's Theorem multiplied by $\sqrt{2}$.

4. The two lines formed in this theorem make $45^\circ$ angles with the lines formed in Van Aubel's Theorem.

5. The two lines formed in this theorem and the two lines from Van Aubel's Theorem intersect at a single point.

---

Second Observation:

In the given figure:

The red line connects the centers of two squares.

The green line connects the centroids of two triangles.

Then, these two lines are perpendicular, and the length of the red line is equal to $1.5 \times$ the length of the green line.

---

If any of these properties are already known, please provide a reference that mentions them. Also, how can we prove these properties?

Thanks!

Answer 1

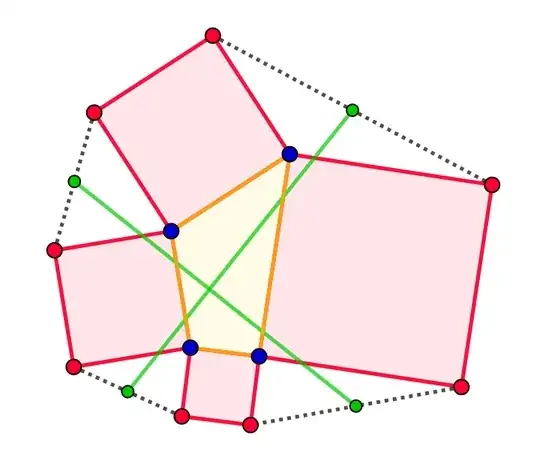
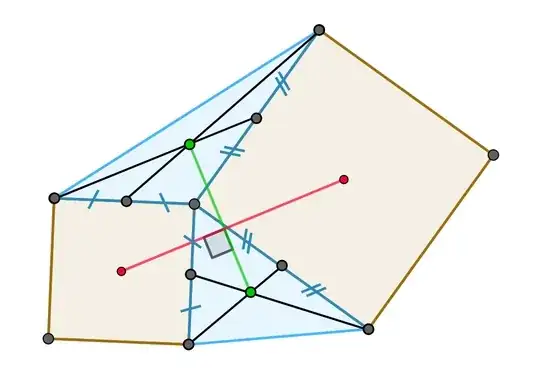
Proof of the property of the first figure.

Let $A_k$, $k=1,...4$ be the vertices of the quadrilateral (numbered in a direct orientation). Let $B_k$ $k=1,...8$ be the vertices of the octagon, beginning in such a way that triangle $A_1B_8B_1$ is one of the triangles of the figure.

Let us use complex number geometry techniques like in this answer, where we make no distinction between a point and the associated complex number.

For example, the geometrical fact that $\vec{A_1B_1}$ is obtained from $\vec{A_1A_2}$ by a $-\pi/2$ rotation, is translated, in the complex domain, into :

$$B_1-A_1=-i(A_2-A_1) \ \iff \ B_1=A_1-i(A_2-A_1)$$

Doing the same kind of computation for each vertex $B_k$ of the exterior octagon (red points), we obtain :

$$\begin{cases} B_1&=&A_1-i(A_2-A_1)\\ B_2&=&A_2-i(A_2-A_1)\\ B_3&=&A_2-i(A_3-A_2)\\ B_4&=&A_3-i(A_3-A_2)\\ B_5&=&A_3-i(A_4-A_3)\\ B_6&=&A_4-i(A_4-A_3)\\ B_7&=&A_4-i(A_1-A_4)\\ B_8&=&A_1-i(A_1-A_4)\end{cases} $$

Therefore, midpoints (green color) are :

$$\begin{cases} M_1&=&A_1+i(A_4-A_2)/2\\ M_2&=&A_2+i(A_1-A_3)/2\\ M_3&=&A_3+i(A_2-A_4)/2\\ M_4&=&A_4+i(A_3-A_1)/2 \end{cases} $$

giving, for the line segments connecting opposite midpoints :

$$\begin{cases}M_3-M_1&=&(A_3-A_1)+i(A_2-A_4)\\M_4-M_2&=&(A_4-A_2)+i(A_3-A_1)\end{cases}$$

Due to the fact that $M_3-M_1=-i(M_4-M_2)$, the orthogonality of line segments $[M_1,M_3]$ and $[M_2,M_4]$ is established.

Two remarks : the figure of your first question represents a case where the initial quadrilateral and the external octagon are convex. As we haven't used at any moment a convexity hypothesis, here are two cases where the given property still holds.

• (fig. 1) Here, though the initial quadrilateral is convex, the exterior octagon isn't convex.

• (fig. 2) In this case, not only the quadrilateral isn't convex, but even more, it is self-intersecting.

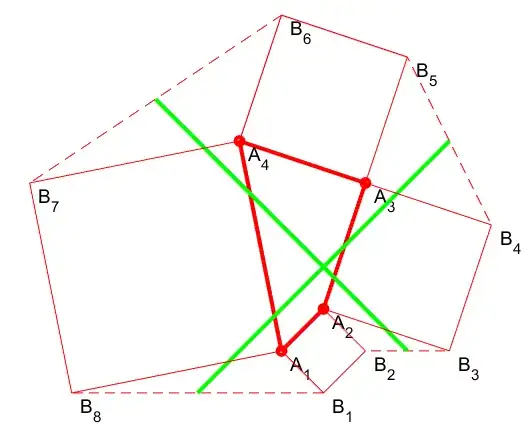
Fig. 1 : A case where the exterior octagon isn't convex.

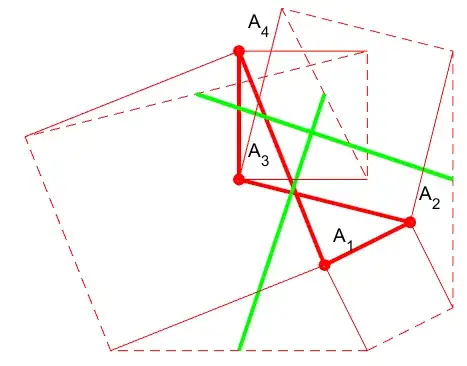
Fig. 2 : A case where the quadrilateral is self-intersecting.

These examples have been obtained with the following Matlab program implementing formulas above :

 clear all;close all
 A=[1+1*i,2+2*i,3+5*i,6*i];A=[A,A(1)];
 V=diff(A);
 plot(A,'-or',LineWidth=3),axis equal off;hold on
 set(gcf,'defaulttextfontsize',14)
 L=A(1:4);d=ones(1,4);
 text(real(L)+0.2*d,imag(L)-0.4*d,{'A_1','A_2','A_3','A_4'})
 for k=1:4
    B(2*k-1)=A(k)-i*V(k);
    B(2*k)=A(k+1)-i*V(k);
 end;
 d=ones(1,8);
 text(real(B)+0.2*d,imag(B)-0.4*d,{'B_1','B_2','B_3','B_4','B_5','B_6','B_7','B_8'});hold on
 plot([B,B(1)],'--r');hold on;
 M(1)=A(1)+i*(A(4)-A(2))/2;
 M(2)=A(2)+i*(A(1)-A(3))/2;
 M(3)=A(3)+i*(A(2)-A(4))/2;
 M(4)=A(4)+i*(A(3)-A(1))/2;

plot([M(1),M(3)],'g',LineWidth=3);hold on plot([M(2),M(4)],'g',LineWidth=3);hold on plot([B(7),B(8),A(1),B(1),B(2),A(2),B(3),B(4),A(3),B(5),B(6),A(4),B(7)],'-r');hold on;