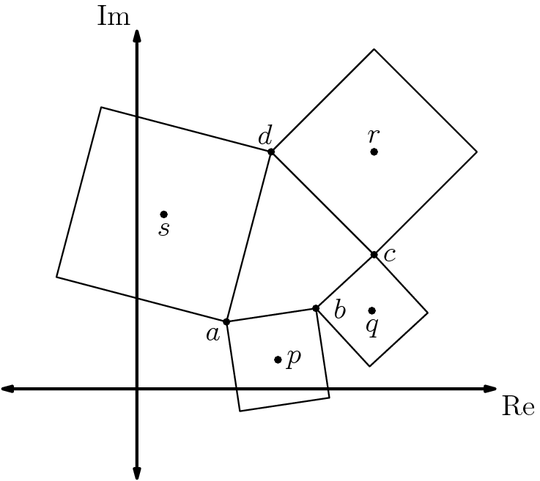
Consider a convex quadrilateral with vertices at $,~,~$ and $$ and on each side draw a square lying outside the given quadrilateral, as in the picture below. Let $,~,~$ and $$ be the centers of those squares:
a) Find expressions for $,~,~$ and $$ in terms of $,~,~$ and $$.
b) Prove that the line segment between $$ and $$ is perpendicular and equal in length to the line segment between $$ and $$.
I think this problem has been asked before, but they don't give any good hints. I don't really know where to start. I tried finding $p$ first by finding $(p-a)$ and $(p-b)$. I tried another way by translating $a$ to the origin. I haven't been able to go farther than this.
I think I have an idea for part $b$ using similar triangles and things, but part a is really confusing.Thank you!
I translated the square with $p$ as its center so that a would be at the origin. So $b$ would then be $b−a$ and $p$ would be $p−a$, right? $p−a$ is half of the diagonal. So then $(p−a)=(b−a)\cdot\frac{\sqrt2}{2}$.
Rotating by $-\frac{\pi}{4}$ would give us $$\frac{(b−a)2}{√2}\cdot e^{−i\frac{\pi}{4}}=\frac{(b−a)\sqrt2}{2}\cdot\left(\frac{\sqrt2}{2}−i\frac{\sqrt2}{2}\right)=\left(\frac{(b−a)}{2}−i\frac{(b−a)}{2}\right)=\frac{b−a−bi+ai}{2}$$ Therefore, $p−a=b−a−bi+ai2$ and when we translate everything back we get $$p=b−a−bi+ai2+a⟹p=b−a−bi+ai+(2a)2⟹p=b+a−bi+ai2.$$ I can do a similar process for the rest of the points, right?
Does it matter which point I translate to the origin?