The minimum $N \times N$ square covering problem for $1 \times 4$ shaped tetrominoes

Question

OK, so me and my friend are working on a problem in which you do the opposite to trying to stuff as many of the I shape tetrominoes in a square as possible. Trying to find the smallest number of I shape tetrominoes that you have to place in the square such that another I shaped tetromino cannot be placed in the square.

So I define $I_n$ to be the sequence such that the rules of the above problem are satisfied.

My friend made a program that finds the values of this sequence. So far we have found that

$I_1 = 0, \ I_2 = 0, \ I_3 = 0, \ I_4 = 4, \ I_5 = 4, \ I_6 = 6, \ I_7 = 7, \ I_8 = 9.$

The problem is that we have got no proofs for any of the cases where $n > 4$.

At first I tried using the pigeonhole principle to try to prove a few cases. For example, when $n = 5$ my argument went a little bit like this.

Lets assume WLOG that an I shaped tetromino was placed in the first row of the square and that a second I shaped tetromino was placed in another row. Now we just place the third shape in the suquare, then that means that there are $5*5 - 4*3 = 13$ remaining free squares. Now using the pigeonhole principle and the assumption of the placement of the first 2 shapes we we get that $13 - 2 = 11$ of the squares are distributed on the 3 rows in which the first $2$ I shapes were not placed. Now by the pigeonhole principle we get that one of the rows must have $\lceil{\frac{11}{3}}\rceil = 4$ free squares. And this is the point where the proof breaks down. I neglected the fact that you can place other I shapes such that even if the row has 4 free squares you still cannot place a new I shape tetromino in it.

So I ask anyone if they have any good ideas that can progress our investigation.

P.S. If you have proofs for your assertions, then please write them out :)

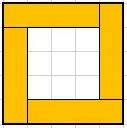
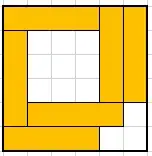
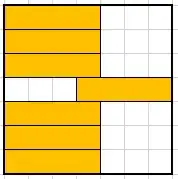
Here I have added visual examples starting from $n = 5$:

$n = 5$

$n = 6$

$n = 7$

$n = 8$

I and my friend are also looking into the same problem with square tetrominoes. I have a general formula for the squares: $\lceil\frac{n-1}{3}\rceil^2$.

My proof starts off by showing how we can do a minimal covering of a $5\times n$ rectangle.

We notice that if we always put new squares in such that they are one cell away from the boundaries of the rectangle and from each other, then looking through a few cases we can come to the conclusion that the formula is $\lceil\frac{n-1}{3}\rceil$.

Now the same principe of being one cell apart from everything else when it can be done also applies for the $n\times n$ case. So then the smallest count would be attained by a certain configuration (I called it the perfect configuration) of the squares. Now it is not hard to notice that the number of squares in the $n \times n$ case is simply the square of the $5 \times n$ case.

My proof basically went along the lines that if you try to remove a square or displace it from the position in which it would be in the perfect configuration, then you could always add a new square, thus gaining a covering that takes up more squares then the perfect configuration one so, therefore the perfect configuration covering must be the minimal.

P.S. If anyone knows any good sources or literature concerning this topic, then please do share them. Thank you!

Answer 1

The "square hole" pattern for $n=5$ can be used to tile the infinite plane resulting in a lower density than $4/7$ achieved by the staircase. Apologies for my poor graphics... :)

. . . B . . . B . . . . A A A A B . . . B . . . B .
. . . B . . . B A A A A B . . . B . . . B . . . B .
. . . B A A A A B . . . B . . . B . . . B A A A A B
A A A A B . . . B . . . B . . . B A A A A B . . . B
B . . . B . . . B . . . B A A A A B . . . B . . . B
B . . . B . . . B A A A A B . . . B . . . B . . . B
B . . . B A A A A B . . . B . . . B . . . B A A A A
B A A A A B . . . B . . . B . . . B A A A A B . . .

The AAAA are the horizontal tiles and the BBBB are the vertical tiles. If my math is right, the density of the plane is the density of this strip:

A A A A B . . . B . . . B . . . B

which works out to be ${8 \over 8+9} = {8 \over 17}$.

I couldnt quite figure out how to achieve the even lower ${7 \over 16}$ mentioned by @PeterTaylor

Answer 2

You can think of this problem as computing the independent domination number of a graph with a node for each of the $2n(n-3)$ tetrominoes and an edge for each pair of tetrominoes that share at least one cell. I used an integer linear programming formulation to confirm your values and find the next several: $I_9=11$, $I_{10}=12$, $I_{11}=16$, $I_{12}=19$, $I_{13}=22$, $I_{14}=26$, $I_{15}=29$. Let $T$ be the set of tetrominoes. For $i,j\in\{1,\dots,n\}$, let $T_{i,j}\subset T$ be the subset of tetrominoes that contain cell $(i,j)$. For $t \in T$, let neighborhood $N_t$ be the set of tetrominoes (including $t$ itself) that share at least one cell with $t$. Let binary decision variable $x_t$ indicate whether tetromino $t\in T$ is used. The problem is to minimize $\sum\limits_{t \in T} x_t$ subject to the following constraints: \begin{align} \sum_{t \in T_{i,j}} x_t &\le 1 &&\text{for $i,j\in\{1,\dots,n\}$} \\ \sum_{\substack{u \in N_t}} x_u &\ge 1 &&\text{for $t\in T$} \\ x_t &\in \{0,1\} &&\text{for $t \in T$} \end{align} The first (independence) constraint prevents more than one tetromino from occupying cell $(i,j)$. The second (domination) constraint forces every tetromino or one of its neighbors to be used.

For the square tetromino variant, the minimum is indeed $\lceil (n-1)/3\rceil^2$. The upper bound is attained by selecting the tetrominoes whose top-left corners are $(3i-2,3j-2)$, where $i,j \in\{1,\dots,\lceil(n-1)/3\rceil\}$. The lower bound arises from the observation that no pair of such cells $(3i-2,3j-2)$ can be dominated by the same tetromino.

Answer 3

I'm expanding here on the comment by Hagen von Eitzen.

On an infinite plane, you can fill it as follows, with "staircases":

They are 3 units apart so there is no room for any further I-tetrominoes. The density of this is obviously $\frac{4}{7}$. A large $n\times n$ square taken from this plane contains about $\frac{4}{7}n^2$ filled cells, or about $\frac{1}{7}n^2$ tetrominoes.

Of course this is not exact for finite boards, because of edge effects - you cannot have partial tetrominoes. You could however simply shift any partial tetrominoes sideways fully into the $n\times n$ square, like this:

This increases the number of filled cells by approximately $\frac{12}{7}n$, but for large $n$ this is negligible compared to the squared term $\frac{4}{7}n^2$ we already have. This general solution gives an upper bound for the number of tetrominoes you need.

No doubt you could work out the exact numbers, finding the optimal placement of these staircases in the square for each large $n$, as they are essentially the same modulo $7$.

The question remains of course whether this is a tight upper bound, i.e. whether the staircase pattern is optimal for large enough $n$, and if so, how large $n$ has to be. For small $n$ the edge effects dominate, and better results are achievable.

Edit: The infinite pattern of squares shown in antkam's answer has a better density, so the starcase pattern is defnitely not optimal for larger $n$. The edge effects are a bit trickier, but still of order $n$, negligable compared to the interior for large $n$.